Site Logo
Smart Growth 101
Search
icon Browse All News
Blog

Where does impervious cover have the biggest impact?

11/11/2019
vector
Tim Evans
Tim Evans
Director of Research
Share
facebook x linkedin

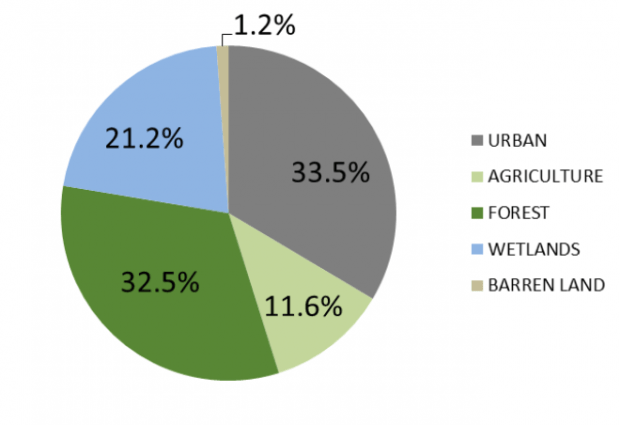
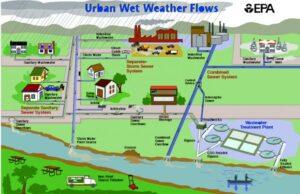
Impervious cover, surfaces such as roads and rooftops that are impenetrable to water, has economic and environmental impacts on municipalities. Streets and sidewalks are expensive to maintain and these surfaces generate stormwater runoff which causes flooding and carries polluted water into our streams and rivers.The New Jersey Department of Environmental Protection (DEP) recently released a 2015 update of its land use / land cover data set.  The LU/LC dataset offers a periodic snapshot of how and where New Jersey both uses and preserves its land.  For example, a little over one-third (33.5 percent) of the state’s land is urbanized and a little less than another third (32.5 percent) is forest, with another 11.6 percent in agricultural use and 21.2 percent in wetlands (and the small remainder classified as “barren land,” a catch-all category that includes things like beaches, quarries, and land that has been cleared for development but on which nothing has yet been built).

image

One feature of interest is the data set’s inclusion of an estimate of impervious surface – things like roads and rooftops that are impervious to water and hence generate stormwater runoff when it rains, rather than allowing water to soak into the ground.  From the data provided for smaller plots of land, it is possible to produce summaries that show how much impervious surface in the state is due to which specific land-use categories. These summaries in turn illustrate an important, though perhaps counterintuitive, point about the environmental benefits of density.Five of the 24 subcategories in the “urban” category of land use pertain to residential development of various types and are described as follows in the metadata:

  • Residential (High Density or Multiple Dwelling): This category contains either high-density single units or multiple dwelling units on 1/8 to 1/5-acre lots. These areas are commonly found in the densely populated urban zones.
  • Residential (Single Unit, Medium Density): This category is made up of residential urban/suburban neighborhoods greater than 1/8 acre and up to and including ½ acre lots.
  • Residential (Single Unit, Low Density):  This category contains single unit residential neighborhoods with areas greater than ½ acre up to and including 1 acre lots.
  • Residential (Rural, Single Unit): This category contains single unit residential neighborhoods with lots that are at least one acre or larger.  This type is typically found in sparsely populated regions surrounded by or adjacent to forested or agricultural lands.  Also included are estates or modern sub-divisions with large lot sizes providing a density less than or equal to one dwelling unit per acre.
  • Mixed Residential: The mixed residential category is used for an area where various residential uses occur and the individual uses cannot be separated at mapping scale (1 acre). Where more than 1/3 intermixture of other residential use or uses occurs in a specific area, it is classified as mixed residential. Where the inter-mixtures of other residential land use or uses total less than 1/3 of the specified area, the dominant land use category is applied.

By summing the total acreage and the impervious acreage for all pieces of land in the database within each of these five subcategories, we can construct estimates of the total amount of New Jersey’s land that is devoted to each of these uses, and what percent of each subcategory’s land is impervious surface:Table 1: Impervious Surface Coverage of Residential Land-Use CategoriesNote that residential development overall devotes 38.8 percent of its acreage to impervious surfaces, on average.  Residential development thus produces slightly less impervious surface per acre than urban land more generally, because other types of urban uses – especially commercial and industrial properties – tend to build out a much higher percent of their lots with buildings and pavement (especially parking lots) and don’t tend to have much in the way of green space.  (A little more than 15 percent of the state’s land area is covered by impervious surfaces overall.)Lawns and wooded areas account for the main difference in impervious surface percent between residential development on one hand and other urban uses on the other.  But they also account for differences among the different subcategories of residential development. Note that among the residential subcategories, the type that generates the most impervious coverage per acre is the highest density category; properties in this category, which tend to be found in the more densely populated urban areas in the state where lawns are both smaller and less common, typically have about 70 percent of their area covered by impervious surfaces.  Even medium-density suburban neighborhoods, with 2 to 8 housing units per acre, devote nearly half (46.8 percent) of their land to impervious surfaces. In contrast, residential development in rural areas that is dominated by single-family detached homes on large lots (1 acre or more) only devotes an average of 20 percent of its total land area to driveways, roofs, and other impervious surfaces.  It may thus appear that the most environmentally-friendly residential form, from the standpoint of generating stormwater runoff, is low-density subdivisions with big lawns and/or lots of trees.But per acre is the wrong denominator to use in measuring residential development’s effect on impervious surface.  When we talk about the future growth of a state, what we are talking about is how many new people or households the state expects to gain over a given time period.  States seek to attract new residents, not new urbanized acreage. The number of new acres a state must develop is a function of how many new people move in, not the other way around.  But the number of newly developed acres is also a function of how we choose to accommodate new population growth.  Will most of it be accommodated via large-lot, single-family development, or via higher-density neighborhoods with apartments, townhouses, and single-family homes on smaller lots?  The types of housing that new residents move into can have widely varying effects on how much new impervious surface gets added per new resident.To keep the math simple, let’s consider a time frame over which New Jersey expects to have to supply 100,000 additional housing units.  As of the 2018 American Community Survey, the average household size – that is, the number of people per occupied housing unit – in New Jersey is 2.69 people.  Using this average, 100,000 new housing units translates to roughly 269,000 new people. This is about equivalent to the amount of population growth that has occurred in New Jersey from 2004 to 2018, a 14-year time frame.  We are thus roughly considering how many new acres of impervious surface we can expect to be generated by about 14 years’ worth of population growth under different residential development scenarios.For each of the four residential land-use categories for which the description specifies a density range, let us pick a representative value for number of units per acre:  10 units per acre for the densest category (this is actually quite a conservative estimate; neighborhoods dominated by rowhouses and apartments will have many more units per acre than 10), 5 units per acre for the medium-density category (which spans from 2 to 8 units per acre), 1.5 units per acre for low-density (lot sizes of between ½ and 1 acre), and 0.5 units per acre for suburban estate developments and rural areas (this corresponds to 2-acre lots; average lot sizes can of course be much larger than this in such developments).  The table below shows what each of these development densities translates to, in terms of number of newly developed acres and thence new acreage of impervious surface.Table 2: Impervious Surfaces Generated by 100,000 New Housing Units Using the average impervious surface coverage rates of the different residential development types, we can see that when measured on a per-capita or per-household basis, rural single-family development produces by far the largest number of new acres of impervious surface for a given population increase; an additional 100,000 households will create 40,000 additional impervious acres.  The highest-density housing types, in contrast, result in the least amount of new impervious surface – less than 7,000 new impervious acres for the same increase of 100,000 households. The tendency of higher-density housing types to cover more of their land area with impervious surfaces is more than made up for by the fact that higher density housing consumes far less acreage per person. If the goal of more environmentally conscious development is to minimize the increase in impervious surface coverage (and thence stormwater runoff) that will be created by a given increase in population size, then, the best way to achieve this is by accommodating as much of the population increase in high-density, rather than low-density, housing types. Similarly, the cost to maintain roads and sidewalks in dense cities is distributed among more people, making dense development a more economic alternative to sprawling communities.

Related Blog

Stormwater Utilities—Peeling Back the Onion

11/26/2025

Stormwater Utilities—Peeling Back the Onion
Urban Centers Are Back! In Fact, So Is the Whole State of New Jersey

08/12/2025

Urban Centers Are Back! In Fact, So Is the Whole State of New Jersey
Navigating New Jersey’s REAL Rules

07/16/2025

Navigating New Jersey’s REAL Rules
When Water Holds Back Housing: What to Expect from New Jersey’s New State Fiscal Year 2026 Intended Use Plans

07/15/2025

When Water Holds Back Housing: What to Expect from New Jersey’s New State Fiscal Year 2026 Intended Use Plans
Farewell Spotlight: Chris Sturm Retires After 23 Years of Championing a Better New Jersey

07/15/2025

Farewell Spotlight: Chris Sturm Retires After 23 Years of Championing a Better New Jersey
Putting the “ART” in SmART Growth

07/01/2025

Putting the “ART” in SmART Growth
New Jersey’s Changing Face: Planning for Intergenerational Households in a Diverse State

07/01/2025

New Jersey’s Changing Face: Planning for Intergenerational Households in a Diverse State
Planning with Purpose: Beth Osborne Calls for Local Leadership and Smart Coalitions

07/01/2025

Planning with Purpose: Beth Osborne Calls for Local Leadership and Smart Coalitions
Building Mobility, Building Prosperity

06/30/2025

Building Mobility, Building Prosperity
Building the Future: Actions to Achieve Great Homes and Neighborhoods in New Jersey and Beyond

06/30/2025

Building the Future: Actions to Achieve Great Homes and Neighborhoods in New Jersey and Beyond
“A Historically High Level of Compliance:” New Jersey Towns Are Making Progress in Meeting Their Affordable Housing Targets

06/30/2025

“A Historically High Level of Compliance:” New Jersey Towns Are Making Progress in Meeting Their Affordable Housing Targets
The Road Ahead: Why Housing Trends Will Shape New Jersey’s Future

06/26/2025

The Road Ahead: Why Housing Trends Will Shape New Jersey’s Future
Clawbacks of Transportation and Green Infrastructure Funding

06/19/2025

Clawbacks of Transportation and Green Infrastructure Funding
From Liberation to Livability: The Deep Connection Between Juneteenth and Urban Development

06/19/2025

From Liberation to Livability: The Deep Connection Between Juneteenth and Urban Development
Walking Together: Honoring Our History, Healing Through Nature, Reimagining What’s Possible

06/16/2025

Walking Together: Honoring Our History, Healing Through Nature, Reimagining What’s Possible
A Tale of Two Upbringings and a Shared Vision For a Healthy Environment

05/21/2025

A Tale of Two Upbringings and a Shared Vision For a Healthy Environment
More Home Choices for New Jersey: How Accessory Dwelling Units Can Help Solve Our Housing Shortage

05/15/2025

More Home Choices for New Jersey: How Accessory Dwelling Units Can Help Solve Our Housing Shortage
Stubborn Seeds and Strong Foundations: What Armenian Resilience Teaches Us About Building Forward

04/22/2025

Stubborn Seeds and Strong Foundations: What Armenian Resilience Teaches Us About Building Forward
More Than Mailers: Keys to Effective Outreach and Communication for Lead Service Line Replacement (LSLR) in New Jersey Communities

04/01/2025

More Than Mailers: Keys to Effective Outreach and Communication for Lead Service Line Replacement (LSLR) in New Jersey Communities
Breaking the Barrier to Water Infrastructure Funding

03/14/2025

Breaking the Barrier to Water Infrastructure Funding
Designing Pedestrian-Friendly Spaces to Enhance Health and Accessibility for New Jersey’s Aging Population

03/13/2025

Designing Pedestrian-Friendly Spaces to Enhance Health and Accessibility for New Jersey’s Aging Population
Debt is Not a Bad Word: Funding New Jersey’s Infrastructure through Smart Financing

02/18/2025

Debt is Not a Bad Word: Funding New Jersey’s Infrastructure through Smart Financing
Exciting Updates to NJ’s State Plan Don’t Miss Your Chance to Speak Up!

02/18/2025

Exciting Updates to NJ’s State Plan Don’t Miss Your Chance to Speak Up!
Breaking Down the State Revolving Fund – Recommendations and Changes

12/02/2024

Breaking Down the State Revolving Fund – Recommendations and Changes
Logging On: Examining the Influence of NUMTOTs on Urbanism Discourse

09/19/2024

Logging On: Examining the Influence of NUMTOTs on Urbanism Discourse
Sustainable and Cost-Efficient: Implementing a Dig-Once Policy in Trenton

08/30/2024

Sustainable and Cost-Efficient: Implementing a Dig-Once Policy in Trenton
Harmful Algal Blooms impacting recreation season for NJ Lakes

07/30/2024

Harmful Algal Blooms impacting recreation season for NJ Lakes
Heat, Air Quality, and Hope: Community Research and Resilience in Elizabeth, NJ

07/30/2024

Heat, Air Quality, and Hope: Community Research and Resilience in Elizabeth, NJ
New Jersey Needs More Housing, and Municipalities are on the Front Lines

07/30/2024

New Jersey Needs More Housing, and Municipalities are on the Front Lines
Stormwater Pays No Mind to Municipal Borders ”Why Should You?

07/30/2024

Stormwater Pays No Mind to Municipal Borders ”Why Should You?
New Jersey’s Housing Landscape: The Mount Laurel Doctrine and the Search for the Missing Middle

07/30/2024

New Jersey’s Housing Landscape: The Mount Laurel Doctrine and the Search for the Missing Middle
New Jersey’s Housing Landscape: The Mount Laurel Doctrine and the Search for the Missing Middle

07/30/2024

New Jersey’s Housing Landscape: The Mount Laurel Doctrine and the Search for the Missing Middle
Municipal Leaders Claim Public Engagement is Largest Asset to Lead Replacement Efforts

06/24/2024

Municipal Leaders Claim Public Engagement is Largest Asset to Lead Replacement Efforts
Unlocking Opportunities: Securing Funding for Trail-Related Projects

06/24/2024

Unlocking Opportunities: Securing Funding for Trail-Related Projects
Making Women’s History Every Month – Meet the Women Board Members at New Jersey Future

03/29/2024

Making Women’s History Every Month – Meet the Women Board Members at New Jersey Future
Making Women’s History Every Month – Meet the Women Board Members at New Jersey Future

03/29/2024

Making Women’s History Every Month – Meet the Women Board Members at New Jersey Future
NJDOT’s Safe Streets to Transit Program Is Improving Communities Across the State “Yours Can Be Next

03/19/2024

NJDOT’s Safe Streets to Transit Program Is Improving Communities Across the State “Yours Can Be Next
NJDOT’s Safe Streets to Transit Program Is Improving Communities Across the State – Yours Can Be Next

03/19/2024

NJDOT’s Safe Streets to Transit Program Is Improving Communities Across the State – Yours Can Be Next
Transit-Oriented Development Is Popular, but Won’t Happen by Itself

03/15/2024

Transit-Oriented Development Is Popular, but Won’t Happen by Itself
New Report Digs Deeper into Diversity in Morris and Monmouth Counties

01/29/2024

New Report Digs Deeper into Diversity in Morris and Monmouth Counties
What You Read 2023 – A Message from the Editor

01/12/2024

What You Read 2023 – A Message from the Editor
Sustainable Water Management: Program Rundown of Municipal Options

12/18/2023

Sustainable Water Management: Program Rundown of Municipal Options
New Jersey Future’s Lame Duck Legislative Priorities for 2023-2024

12/05/2023

New Jersey Future’s Lame Duck Legislative Priorities for 2023-2024
New Jersey Future’s Lame Duck Legislative Priorities for 2023-2024

12/05/2023

New Jersey Future’s Lame Duck Legislative Priorities for 2023-2024
The Future of Housing in New Jersey

11/30/2023

The Future of Housing in New Jersey
The NJ State Development and Redevelopment Plan is Being Updated – Where and How Should New Jersey Grow? Add Your Voice!

10/12/2023

The NJ State Development and Redevelopment Plan is Being Updated – Where and How Should New Jersey Grow? Add Your Voice!
Green Infrastructure in the Garden State: Stormwater Research in the Delaware River Watershed

09/20/2023

Green Infrastructure in the Garden State: Stormwater Research in the Delaware River Watershed
Accessing New Federal Funding for Active Transportation Projects: Camden County Got a Bunch, How Can You?

09/18/2023

Accessing New Federal Funding for Active Transportation Projects: Camden County Got a Bunch, How Can You?
Creating Safe Communities and Options for Walk-Bike-Ride Transportation in New Jersey

08/08/2023

Creating Safe Communities and Options for Walk-Bike-Ride Transportation in New Jersey
Rethinking Colonial Narratives and Transforming Native Insight into Actions: Indigenous Preservation of History

07/20/2023

Rethinking Colonial Narratives and Transforming Native Insight into Actions: Indigenous Preservation of History
With Recession in the Forecast, How Prepared is NJ’s Economy for Upcoming Rain?

07/20/2023

With Recession in the Forecast, How Prepared is NJ’s Economy for Upcoming Rain?
Promoting Integration at the Local Level

07/20/2023

Promoting Integration at the Local Level
Landmarking the Legacy of NJ Transgender Icon, Venus Pellagatii Xtravaganza

07/20/2023

Landmarking the Legacy of NJ Transgender Icon, Venus Pellagatii Xtravaganza
Next Stop: Transit Friendly Communities and TOD Opportunities

07/20/2023

Next Stop: Transit Friendly Communities and TOD Opportunities
The Changing Faces of New Jersey Developers

07/18/2023

The Changing Faces of New Jersey Developers
Planning for Tomorrow, Not Today

07/18/2023

Planning for Tomorrow, Not Today
Hinchliffe Stadium Opens New Opportunities for Paterson while Reconnecting to its Past

07/18/2023

Hinchliffe Stadium Opens New Opportunities for Paterson while Reconnecting to its Past
Launching the Next State Plan

07/18/2023

Launching the Next State Plan
Examining the Influence of 50 years of Hip Hop on Planning and Redevelopment

07/18/2023

Examining the Influence of 50 years of Hip Hop on Planning and Redevelopment
Common Ground Emerges on Affordable Housing Solutions

07/17/2023

Common Ground Emerges on Affordable Housing Solutions
Ch-Ch-Ch-Changes! How Water Utilities and Communities are Addressing Changing Climate, Changing Regulations and Changing Lead Pipes!

07/17/2023

Ch-Ch-Ch-Changes! How Water Utilities and Communities are Addressing Changing Climate, Changing Regulations and Changing Lead Pipes!
Planning for Climate Resilient Stormwater Infrastructure

07/17/2023

Planning for Climate Resilient Stormwater Infrastructure
Five Community Planning Initiatives To Solve Problems and Save Money

06/06/2023

Five Community Planning Initiatives To Solve Problems and Save Money
New Report Highlights Link Between Local Zoning and Housing Affordability

05/17/2023

New Report Highlights Link Between Local Zoning and Housing Affordability
Rolling Along: Why New Jersey Should Join Other States and Offer an E-Bike Incentive Program

05/17/2023

Rolling Along: Why New Jersey Should Join Other States and Offer an E-Bike Incentive Program
Eliminating Lead Service Lines: Filling the Funding Gap, One Drop at a Time

05/11/2023

Eliminating Lead Service Lines: Filling the Funding Gap, One Drop at a Time
Transportation for Everyone: Designing Safe, Sustainable Options for Women

03/17/2023

Transportation for Everyone: Designing Safe, Sustainable Options for Women
Metuchen’s Downtown Revitalization: An Award-Winning Catalyst for Smart Growth

03/16/2023

Metuchen’s Downtown Revitalization: An Award-Winning Catalyst for Smart Growth
New Jersey Future (NJF) at the White House

02/06/2023

New Jersey Future (NJF) at the White House
Helping NJ Drive Less: The Need to Dedicate Funding to Transit and Safe Streets

01/31/2023

Helping NJ Drive Less: The Need to Dedicate Funding to Transit and Safe Streets
Transit-Oriented Development is Pedestrian-Oriented Development

01/30/2023

Transit-Oriented Development is Pedestrian-Oriented Development
2023 NJ Planning and Redevelopment Conference

01/20/2023

2023 NJ Planning and Redevelopment Conference
Vacant Housing Tells Sprawl Story, Too

01/17/2023

Vacant Housing Tells Sprawl Story, Too
New NJDEP Watershed Improvement Plan Requirement and What This Means for Municipalities

01/04/2023

New NJDEP Watershed Improvement Plan Requirement and What This Means for Municipalities
Opinion: Car-Free Inspiration From an Overseas Adventure

05/01/2023

Opinion: Car-Free Inspiration From an Overseas Adventure
Access to Parks is an Environmental Justice Issue

04/19/2023

Access to Parks is an Environmental Justice Issue
From Federal Dollars to State Investment: Understanding Technical Assistance for Water Systems

04/17/2023

From Federal Dollars to State Investment: Understanding Technical Assistance for Water Systems
NJDEP Finalizes Water Infrastructure Investment Priorities for 2023

11/29/2022

NJDEP Finalizes Water Infrastructure Investment Priorities for 2023
PFAS in the Garden State: What It Is and What We’re Doing About It

11/11/2022

PFAS in the Garden State: What It Is and What We’re Doing About It
Ten Years After Sandy, a Look at Population and Housing Trends at the Jersey Shore

10/25/2022

Ten Years After Sandy, a Look at Population and Housing Trends at the Jersey Shore
New Jersey Future Shapes and Supports New Flood Disclosure Legislation

10/21/2022

New Jersey Future Shapes and Supports New Flood Disclosure Legislation
Clean Water in the Garden State: Reflecting on 50 years of Progress and Challenges

10/18/2022

Clean Water in the Garden State: Reflecting on 50 years of Progress and Challenges
New NJF Report Explores How to Promote Racial Integration in NJ Municipalities

09/22/2022

New NJF Report Explores How to Promote Racial Integration in NJ Municipalities
Next Steps for Warehouse Planning – and Regional Planning More Broadly

09/21/2022

Next Steps for Warehouse Planning – and Regional Planning More Broadly
New Jersey Future Provides Direction at Joint State Senate and State Assembly Climate Hearing

08/16/2022

New Jersey Future Provides Direction at Joint State Senate and State Assembly Climate Hearing
Meet New Jersey Future’s 2022 Summer Interns!

08/09/2022

Meet New Jersey Future’s 2022 Summer Interns!
Amidst rising pedestrian and traffic fatalities, New Jersey seeks to advance safe street design

07/19/2022

Amidst rising pedestrian and traffic fatalities, New Jersey seeks to advance safe street design
Opportunity to Participate in a Pilot Program to Track Vehicle Miles Traveled in New Jersey

07/19/2022

Opportunity to Participate in a Pilot Program to Track Vehicle Miles Traveled in New Jersey
The Risk to Our Roofs: Considering and Harnessing the Climate-Housing Nexus

07/11/2022

The Risk to Our Roofs: Considering and Harnessing the Climate-Housing Nexus
The State of New Jersey’s Housing Market: We Need More

07/11/2022

The State of New Jersey’s Housing Market: We Need More
State Agencies Shape Infrastructure Programs to Address 21st Century Challenges

07/11/2022

State Agencies Shape Infrastructure Programs to Address 21st Century Challenges
Social Determinants of Health: National and Local Perspectives

07/11/2022

Social Determinants of Health: National and Local Perspectives
Warehouse Development: Regional Significance Calls for Regional Perspective

07/11/2022

Warehouse Development: Regional Significance Calls for Regional Perspective
Walking the Talk: Planning for Places that Actualize Equity and Inclusion

07/08/2022

Walking the Talk: Planning for Places that Actualize Equity and Inclusion
Equitable, Sustainable Development and Redevelopment for a Bright New Jersey Future

07/08/2022

Equitable, Sustainable Development and Redevelopment for a Bright New Jersey Future
Constructing Accessible and Inclusive Communities for People with Disabilities

07/08/2022

Constructing Accessible and Inclusive Communities for People with Disabilities
Beyond Getting from A to B: Ensuring Safer and Fairer Ways to Move Around

07/08/2022

Beyond Getting from A to B: Ensuring Safer and Fairer Ways to Move Around
Demonstration Projects: Seeing is Believing Doing is Achieving

07/08/2022

Demonstration Projects: Seeing is Believing Doing is Achieving
Reducing Rain’s Repercussions: Exploring the Potential for Green Infrastructure on Redevelopment Sites

07/08/2022

Reducing Rain’s Repercussions: Exploring the Potential for Green Infrastructure on Redevelopment Sites
Reducing Rain’s Repercussions: Exploring the Potential for Green Infrastructure on Redevelopment Sites

07/08/2022

Reducing Rain’s Repercussions: Exploring the Potential for Green Infrastructure on Redevelopment Sites
Lead by Example: Equitably Addressing the Toxic Lead Issues in Your Town

07/07/2022

Lead by Example: Equitably Addressing the Toxic Lead Issues in Your Town
Centering Small Business in Post-Pandemic Redevelopment

07/07/2022

Centering Small Business in Post-Pandemic Redevelopment
Award-Winning Map Shows Water-Related Environmental Justice Issues in New Jersey

06/30/2022

Award-Winning Map Shows Water-Related Environmental Justice Issues in New Jersey
Street View: Fostering an Inclusive Community Through Complete and Green Streets

06/29/2022

Street View: Fostering an Inclusive Community Through Complete and Green Streets
One Year Later: How NJ Municipalities Have Implemented DEP’s Stormwater Management Rules

06/27/2022

One Year Later: How NJ Municipalities Have Implemented DEP’s Stormwater Management Rules
Making Savvy, Successful Stormwater Solutions: Why the Municipal Separate Storm Sewer (MS4) Permit Renewal Matters

06/24/2022

Making Savvy, Successful Stormwater Solutions: Why the Municipal Separate Storm Sewer (MS4) Permit Renewal Matters
Young People are Leaving New Jersey: Exploring Potential Explanatory Variables

06/22/2022

Young People are Leaving New Jersey: Exploring Potential Explanatory Variables
State Guidance for Locating Warehouses is Here

06/10/2022

State Guidance for Locating Warehouses is Here
We Need a Better Way of Measuring How Much People Drive And Why

05/23/2022

We Need a Better Way of Measuring How Much People Drive And Why
Supporting Equitable Access to Transit and Active Transportation

05/23/2022

Supporting Equitable Access to Transit and Active Transportation
Community Design for All Ages: A New Sustainable Jersey Municipal Action

05/20/2022

Community Design for All Ages: A New Sustainable Jersey Municipal Action
If You Pave It, They Will Park

04/25/2022

If You Pave It, They Will Park
Complete Street and Goods Delivery: What Is a Street For?

03/24/2022

Complete Street and Goods Delivery: What Is a Street For?
Crossroads in New Jersey: Investing in Water Infrastructure “Post-Newark”

02/22/2022

Crossroads in New Jersey: Investing in Water Infrastructure “Post-Newark”
Walking and Biking Are Transportation Too

02/18/2022

Walking and Biking Are Transportation Too
New Resources to Drive New Jersey Toward Green Street Implementation

01/19/2022

New Resources to Drive New Jersey Toward Green Street Implementation
Environmental Justice and Warehouse Sprawl

12/07/2021

Environmental Justice and Warehouse Sprawl
From Planning With Purpose to Action for All Ages

12/02/2021

From Planning With Purpose to Action for All Ages
NJ Residents can Improve Flood Management, one Rain Garden at a Time

11/01/2021

NJ Residents can Improve Flood Management, one Rain Garden at a Time
Electric Yard Goats and Environmental Justice

10/13/2021

Electric Yard Goats and Environmental Justice
Hispanic Heritage Month and the Growth of New Jersey’s Latinx Population

10/13/2021

Hispanic Heritage Month and the Growth of New Jersey’s Latinx Population
School district regionalization is an educational quality issue”and a cost-saving issue, and a land-use issue, and a segregation issue

10/13/2021

School district regionalization is an educational quality issue”and a cost-saving issue, and a land-use issue, and a segregation issue
Lead Exposure: Learning From East Trenton Residents

09/13/2021

Lead Exposure: Learning From East Trenton Residents
New Jersey Municipalities Share Green Infrastructure Planning Progress

09/13/2021

New Jersey Municipalities Share Green Infrastructure Planning Progress
Census 2020: New Jersey’s Older and Increasingly Diverse Centers Are Now Leading The State’s Population Growth

09/13/2021

Census 2020: New Jersey’s Older and Increasingly Diverse Centers Are Now Leading The State’s Population Growth
Lead in Drinking Water in Public Schools: State Assistance Accelerates the Solution in New Jersey

09/13/2021

Lead in Drinking Water in Public Schools: State Assistance Accelerates the Solution in New Jersey
New Jersey Needs More “Missing Middle” Housing

07/19/2021

New Jersey Needs More “Missing Middle” Housing
New Jersey Behind the Curve on Broadband Funding

07/19/2021

New Jersey Behind the Curve on Broadband Funding
Strategizing from Sussex to Stone Harbor: Water Infrastructure in New Jersey’s Climate Strategy

07/19/2021

Strategizing from Sussex to Stone Harbor: Water Infrastructure in New Jersey’s Climate Strategy
New Jersey Needs More “Missing Middle” Housing

07/19/2021

New Jersey Needs More “Missing Middle” Housing
Filling the Missing Middle: Context-Sensitive Design and Development Innovations for Diverse, Sustainable, Walkable Neighborhoods

06/25/2021

Filling the Missing Middle: Context-Sensitive Design and Development Innovations for Diverse, Sustainable, Walkable Neighborhoods
Oh, Sweet Relief! Stormwater Utilities as an Equitable Tool to Solve Flooding and Pollution

06/25/2021

Oh, Sweet Relief! Stormwater Utilities as an Equitable Tool to Solve Flooding and Pollution
Savvy Stormwater Strategies: How Planning at Every Level Can Help New Jersey Weather the Storm

06/25/2021

Savvy Stormwater Strategies: How Planning at Every Level Can Help New Jersey Weather the Storm
Ensuring Equity in Transit-Oriented Development

06/25/2021

Ensuring Equity in Transit-Oriented Development
Municipal Approach to Racial and Economic Inclusion

06/25/2021

Municipal Approach to Racial and Economic Inclusion
How to Reinvigorate Retail-Anchored Downtowns in a Post-Pandemic World

06/25/2021

How to Reinvigorate Retail-Anchored Downtowns in a Post-Pandemic World
The Future of New Jersey: An Economic Forecast

06/25/2021

The Future of New Jersey: An Economic Forecast
Web Mapping to Support Smart Equitable Cities in Community Planning

06/25/2021

Web Mapping to Support Smart Equitable Cities in Community Planning
Creating Aging-Friendly Communities Through Municipal Actions and Partnerships

06/25/2021

Creating Aging-Friendly Communities Through Municipal Actions and Partnerships
Community Benefits Agreements: Understanding the New Requirement and How to Create a Win-Win

06/25/2021

Community Benefits Agreements: Understanding the New Requirement and How to Create a Win-Win
Two Homes, One Roof: Making NJ More Welcoming with ADUs

06/25/2021

Two Homes, One Roof: Making NJ More Welcoming with ADUs
Geography of Equity and Inclusion: The Big Picture

06/24/2021

Geography of Equity and Inclusion: The Big Picture
Water, Water Everywhere—Achilles Heel or Asset?

06/24/2021

Water, Water Everywhere—Achilles Heel or Asset?
Incorporating Climate Change: It’s the Law

06/24/2021

Incorporating Climate Change: It’s the Law
Tracking Progress on Environmental Justice

06/15/2021

Tracking Progress on Environmental Justice
All Boats Rise: Investing in Climate Resilience & Communities

06/15/2021

All Boats Rise: Investing in Climate Resilience & Communities
New Jersey Future and Partners Launch Lead-Free NJ

06/15/2021

New Jersey Future and Partners Launch Lead-Free NJ
Hoboken’s Focus on Vision Zero Makes Streets Safe for Everyone

05/06/2021

Hoboken’s Focus on Vision Zero Makes Streets Safe for Everyone
A New Housing Model for New Jersey

05/04/2021

A New Housing Model for New Jersey
New Jersey Future Urges Congressional Delegation to Secure Funding for Lead Service Line Replacement

04/30/2021

New Jersey Future Urges Congressional Delegation to Secure Funding for Lead Service Line Replacement
NJDEP Releases Guidance on Stormwater Utilities, a Tool for Equitable Stormwater Management

04/12/2021

NJDEP Releases Guidance on Stormwater Utilities, a Tool for Equitable Stormwater Management
Single-Family Zoning: An Idea Whose Time Has Passed?

04/12/2021

Single-Family Zoning: An Idea Whose Time Has Passed?
School District Consolidation Is More Than Just a Cost-Saving Measure

04/12/2021

School District Consolidation Is More Than Just a Cost-Saving Measure
Can the Reduction in Travel Prompted by COVID-19 Be Sustained?

03/15/2021

Can the Reduction in Travel Prompted by COVID-19 Be Sustained?
Warehouse Sprawl: Plan Now or Suffer the Consequences

03/15/2021

Warehouse Sprawl: Plan Now or Suffer the Consequences
New Jersey Future’s Comments on CSO Long Term Control Plans

03/15/2021

New Jersey Future’s Comments on CSO Long Term Control Plans
New Stormwater Rules Require New Developments to Include Green Infrastructure

03/05/2021

New Stormwater Rules Require New Developments to Include Green Infrastructure
Where Do New Jersey’s Property Tax Bills Hit the Hardest?

02/15/2021

Where Do New Jersey’s Property Tax Bills Hit the Hardest?
Helping towns design for all ages: New Jersey Future’s aging-friendly program is gaining momentum

02/15/2021

Helping towns design for all ages: New Jersey Future’s aging-friendly program is gaining momentum
Continuing Implications of Broadband Inequity

02/11/2021

Continuing Implications of Broadband Inequity
Older Homeowners in Car-Dependent Suburbs Face Difficulty Downsizing

02/11/2021

Older Homeowners in Car-Dependent Suburbs Face Difficulty Downsizing
New Jersey Future and other Jersey Water Works Members Call for Federal Funding for Water Infrastructure

02/10/2021

New Jersey Future and other Jersey Water Works Members Call for Federal Funding for Water Infrastructure
Want to Get Ahead of Flooding? Use NJF’s New Tool, the Enhanced Model Stormwater Ordinance

02/09/2021

Want to Get Ahead of Flooding? Use NJF’s New Tool, the Enhanced Model Stormwater Ordinance
New Jersey Future Releases Guide to Implementing Aging-Friendly Land Use Decisions

01/15/2021

New Jersey Future Releases Guide to Implementing Aging-Friendly Land Use Decisions
New Jersey Future analysis of the New Jersey Economic Recovery Act of 2020

12/21/2020

New Jersey Future analysis of the New Jersey Economic Recovery Act of 2020
New Jersey’s population impacted by loss of immigrants

08/06/2020

New Jersey’s population impacted by loss of immigrants
New Jersey’s population impacted by loss of immigrants

08/06/2020

New Jersey’s population impacted by loss of immigrants
What’s in your water? A new dashboard will help you find out.

07/14/2020

What’s in your water? A new dashboard will help you find out.
What’s in your water? A new dashboard will help you find out.

07/14/2020

What’s in your water? A new dashboard will help you find out.
What’s in your water? A new dashboard will help you find out.

07/14/2020

What’s in your water? A new dashboard will help you find out.
Newark’s Lead Service Line Replacement Program is a Model for the Nation

06/12/2020

Newark’s Lead Service Line Replacement Program is a Model for the Nation
Let’s Not Go Backward. Let’s Rebuild Better As We Recover

05/26/2020

Let’s Not Go Backward. Let’s Rebuild Better As We Recover
Looking to New Jersey’s Future

04/19/2020

Looking to New Jersey’s Future
It’s Official: NJDEP Amends State Stormwater Rules to Require Green Infrastructure

03/11/2020

It’s Official: NJDEP Amends State Stormwater Rules to Require Green Infrastructure
It’s Official: NJDEP Amends State Stormwater Rules to Require Green Infrastructure

03/11/2020

It’s Official: NJDEP Amends State Stormwater Rules to Require Green Infrastructure
It’s Official: NJDEP’s Stormwater Rule Changes Published in the New Jersey Register

03/02/2020

It’s Official: NJDEP’s Stormwater Rule Changes Published in the New Jersey Register
It’s Official: NJDEP’s Stormwater Rule Changes Published in the New Jersey Register

03/02/2020

It’s Official: NJDEP’s Stormwater Rule Changes Published in the New Jersey Register
New Jersey’s Supply of Developable Land Is Shrinking As a Result of Both Development and Preservation

02/17/2020

New Jersey’s Supply of Developable Land Is Shrinking As a Result of Both Development and Preservation
Stuck with Stormwater Issues? See Expert Solutions to Fight Flooding and Pollution in the Updated Municipal Toolkit

11/10/2020

Stuck with Stormwater Issues? See Expert Solutions to Fight Flooding and Pollution in the Updated Municipal Toolkit
Visualizing an Aging-Friendly Built Environment for Implementation in Ridgewood Village

11/10/2020

Visualizing an Aging-Friendly Built Environment for Implementation in Ridgewood Village
Does School District Fragmentation Support Residential Segregation?

11/09/2020

Does School District Fragmentation Support Residential Segregation?
Stormwater Utilities—Peeling Back the Onion

11/09/2020

Stormwater Utilities—Peeling Back the Onion
An Interview with 2020 Cary Edwards Leadership Award Winner Peter Reinhart

11/09/2020

An Interview with 2020 Cary Edwards Leadership Award Winner Peter Reinhart
To Reduce Greenhouse Gas Emissions, We Need to Drive Less—and Build Smarter

10/14/2020

To Reduce Greenhouse Gas Emissions, We Need to Drive Less—and Build Smarter
Changes to Municipal Land Use Law would make NJ municipalities more resilient

10/14/2020

Changes to Municipal Land Use Law would make NJ municipalities more resilient
The Geography of Poverty and Race in New Jersey

10/14/2020

The Geography of Poverty and Race in New Jersey
New Jersey Future Partners with the New Jersey District of Key Club International

10/14/2020

New Jersey Future Partners with the New Jersey District of Key Club International
Broadband for All: The Geography of Digital Equity in New Jersey

09/16/2020

Broadband for All: The Geography of Digital Equity in New Jersey
The Black-White Homeownership Gap in New Jersey

09/16/2020

The Black-White Homeownership Gap in New Jersey
Greening the Garden State: These Three Towns Show You How!Â

09/15/2020

Greening the Garden State: These Three Towns Show You How!Â
Meet our 2020 Summer Interns!

09/15/2020

Meet our 2020 Summer Interns!
New Jersey Future Launches the New Jersey Stormwater Utilities Resource Center

09/04/2020

New Jersey Future Launches the New Jersey Stormwater Utilities Resource Center
A Guide to Diversifying Housing Options for an Aging Population

08/11/2020

A Guide to Diversifying Housing Options for an Aging Population
A Shift to Working From Home Raises Many Questions About Potential Effects on Other Aspects of Daily Life

08/06/2020

A Shift to Working From Home Raises Many Questions About Potential Effects on Other Aspects of Daily Life
New Jersey Future to work with regional campaign for resilience

07/14/2020

New Jersey Future to work with regional campaign for resilience
Meet our 2020 Spring Interns!

07/14/2020

Meet our 2020 Spring Interns!
Bolstering the Water Workforce with Innovative Programs

06/12/2020

Bolstering the Water Workforce with Innovative Programs
Redevelopment Is the New Normal

06/12/2020

Redevelopment Is the New Normal
Public-Private Partnerships Are a Valuable Tool for Expanding Housing

06/10/2020

Public-Private Partnerships Are a Valuable Tool for Expanding Housing
New Jersey Future, New Jersey Builders Association release updated Developers Green Infrastructure Guide

06/05/2020

New Jersey Future, New Jersey Builders Association release updated Developers Green Infrastructure Guide
United in the Fight for Equity and Justice

06/03/2020

United in the Fight for Equity and Justice
How to Strengthen a COVID-19 Small Business Program

05/26/2020

How to Strengthen a COVID-19 Small Business Program
New Jersey Future Welcomes Four New Trustees

05/06/2020

New Jersey Future Welcomes Four New Trustees
Urban Comeback in New Jersey

05/05/2020

Urban Comeback in New Jersey
Aging-friendly housing options: A case study

05/05/2020

Aging-friendly housing options: A case study
NJ Stay-at-Home Order is Reducing GHG Emissions

04/15/2020

NJ Stay-at-Home Order is Reducing GHG Emissions
With the Parks Closed, Now is the Time to Open the Streets

04/15/2020

With the Parks Closed, Now is the Time to Open the Streets
Looking to New Jersey’s Future

04/09/2020

Looking to New Jersey’s Future
New Jersey Future and NJDEP release report of local options and actions for resilience

03/13/2020

New Jersey Future and NJDEP release report of local options and actions for resilience
Smart Growth Gets Smarter

03/11/2020

Smart Growth Gets Smarter
The Best Is Yet To Come: New Jersey Future Helps Towns Become Great Places to Age

03/09/2020

The Best Is Yet To Come: New Jersey Future Helps Towns Become Great Places to Age
Climate-Ready CSO Solutions Forum

02/20/2020

Climate-Ready CSO Solutions Forum
Does the Retail Apocalypse Mean the End of Downtowns?

02/17/2020

Does the Retail Apocalypse Mean the End of Downtowns?
New Jersey Losing Population for the First Time in Four Decades

01/16/2020

New Jersey Losing Population for the First Time in Four Decades
2020 Redevelopment Forum

01/14/2020

2020 Redevelopment Forum
Deadline Extended to May 31! Apply for a 2020 Smart Growth Award

01/13/2020

Deadline Extended to May 31! Apply for a 2020 Smart Growth Award
Resilience planning in Medford

01/07/2020

Resilience planning in Medford
New Jersey’s Board of Public Utilities Energy Master Plan Stakeholder Meetings

09/04/2019

New Jersey’s Board of Public Utilities Energy Master Plan Stakeholder Meetings
New Jersey Future staff explore Paterson

08/13/2019

New Jersey Future staff explore Paterson
Is New Jersey’s Water Safe to Drink?

05/06/2019

Is New Jersey’s Water Safe to Drink?
New County Population Estimates: More of the Same Changes

04/24/2019

New County Population Estimates: More of the Same Changes
Main Street New Jersey Regional Workshop – Red Bank

03/22/2019

Main Street New Jersey Regional Workshop – Red Bank
2019 EPA OCR Strategies for Food Systems, Health, and Economic Development Webinar

03/18/2019

2019 EPA OCR Strategies for Food Systems, Health, and Economic Development Webinar
New Jersey’s Approval Rate Sinking With Young Adults

03/13/2019

New Jersey’s Approval Rate Sinking With Young Adults
Ecology & Economy: Resolving Our Climate Crisis

03/01/2019

Ecology & Economy: Resolving Our Climate Crisis
WEBINAR – The Rise of Freelance Artists: Implications for Urban Planning and Design

03/01/2019

WEBINAR – The Rise of Freelance Artists: Implications for Urban Planning and Design
Designing Sites for Creativity

03/01/2019

Designing Sites for Creativity
What Kinds of Places Are Attracting New Jersey’s Out-migrating Millennials?

02/26/2019

What Kinds of Places Are Attracting New Jersey’s Out-migrating Millennials?
New Jersey Future’s David Kutner To Receive Statewide Planning Award

01/14/2019

New Jersey Future’s David Kutner To Receive Statewide Planning Award
New Population Estimates: New Jersey’s Still Growing, But Slowly

01/02/2019

New Population Estimates: New Jersey’s Still Growing, But Slowly
New Population Estimates: New Jersey’s Still Growing, But Slowly

01/02/2019

New Population Estimates: New Jersey’s Still Growing, But Slowly
Planning for Aging-Friendliness in Fair Lawn Borough

12/17/2019

Planning for Aging-Friendliness in Fair Lawn Borough
Free event! Learn how CSO plans can address climate change

12/12/2019

Free event! Learn how CSO plans can address climate change
Climate-Ready Combined Sewer Overflow Solutions Forum

12/11/2019

Climate-Ready Combined Sewer Overflow Solutions Forum
Celebrating the 20th Anniversary of New Jersey’s Transit Village Program

12/09/2019

Celebrating the 20th Anniversary of New Jersey’s Transit Village Program
Addressing urban challenges at the APA Policy and Advocacy Conference

11/11/2019

Addressing urban challenges at the APA Policy and Advocacy Conference
Mayors Panel on Water Quality

11/06/2019

Mayors Panel on Water Quality
Lead in Drinking Water Webinar

11/06/2019

Lead in Drinking Water Webinar
Strong Towns: East Orange

10/25/2019

Strong Towns: East Orange
2019 New Jersey Non-Profit Conference

10/18/2019

2019 New Jersey Non-Profit Conference
The Residential Revolution

10/17/2019

The Residential Revolution
2019 Complete Streets Summit

10/15/2019

2019 Complete Streets Summit
Local Implementation Planning in Ridgewood Village Will Help Create Great Places to Age in New Jersey

10/14/2019

Local Implementation Planning in Ridgewood Village Will Help Create Great Places to Age in New Jersey
Trenton Holds its First Ciclovia

10/14/2019

Trenton Holds its First Ciclovia
Three Lessons for Reinventing the Suburbs

10/11/2019

Three Lessons for Reinventing the Suburbs
Where are the lead service lines in New Jersey?

10/03/2019

Where are the lead service lines in New Jersey?
Clean Water Council Public Hearing

09/25/2019

Clean Water Council Public Hearing
Third Annual “Building a Culture of Health” Conference

09/23/2019

Third Annual “Building a Culture of Health” Conference
WEBINAR: The Missing Middle and Missing Little – Creating Housing Diversity for All Incomes and Stages of Life

09/09/2019

WEBINAR: The Missing Middle and Missing Little – Creating Housing Diversity for All Incomes and Stages of Life
Understanding Advanced Stormwater Management Techniques – Green Infrastructure Applications

09/06/2019

Understanding Advanced Stormwater Management Techniques – Green Infrastructure Applications
Wetland Construction: Principles, Planning and Design

09/06/2019

Wetland Construction: Principles, Planning and Design
Health Impact Assessment: Incorporating Health into Planning and Decision-Making

09/06/2019

Health Impact Assessment: Incorporating Health into Planning and Decision-Making
Fight flooding and pollution with the updated Green Infrastructure Municipal Toolkit

09/05/2019

Fight flooding and pollution with the updated Green Infrastructure Municipal Toolkit
ANJEC Annual Environmental Congress

09/04/2019

ANJEC Annual Environmental Congress
Sustainable Jersey Listening Session

09/04/2019

Sustainable Jersey Listening Session
WEBINAR: Gardinier Energy Grant Informational Webinar

09/04/2019

WEBINAR: Gardinier Energy Grant Informational Webinar
Green infrastructure resource wins national award

09/03/2019

Green infrastructure resource wins national award
Pennsylvania Automated Vehicle Summit 2019

08/28/2019

Pennsylvania Automated Vehicle Summit 2019
Healthy Schools Now Coalition Meeting

08/28/2019

Healthy Schools Now Coalition Meeting
Stormwater Camp? Yes please!

08/26/2019

Stormwater Camp? Yes please!
Time for public input on sewer solutions

08/19/2019

Time for public input on sewer solutions
Build streets for everyone with this new model policy

08/13/2019

Build streets for everyone with this new model policy
explore Paterson

08/13/2019

explore Paterson
Meet our summer 2019 interns!

08/12/2019

Meet our summer 2019 interns!
Program manager Jyoti Venketraman to be honored

08/12/2019

Program manager Jyoti Venketraman to be honored
Downtown Management Round Table (Sept 2019 Luncheon)

08/09/2019

Downtown Management Round Table (Sept 2019 Luncheon)
Increasing Analytical Laboratory Preparedness

08/09/2019

Increasing Analytical Laboratory Preparedness
4th Annual Healthy Homes and Communities Summit

07/29/2019

4th Annual Healthy Homes and Communities Summit
WEBINAR: Designing for Resilience Across Scales, Systems and Sectors

07/19/2019

WEBINAR: Designing for Resilience Across Scales, Systems and Sectors
US Green Building Council NJ’s 16th Annual Golf Outing

07/19/2019

US Green Building Council NJ’s 16th Annual Golf Outing
USGBC NJ Annual Summer Social & Member Reception

07/19/2019

USGBC NJ Annual Summer Social & Member Reception
New Jersey’s Board of Public Utilities Energy Master Plan Stakeholder Meetings 3&4

07/17/2019

New Jersey’s Board of Public Utilities Energy Master Plan Stakeholder Meetings 3&4
New Jersey’s Board of Public Utilities Energy Master Plan Stakeholder Meetings 1&2

07/17/2019

New Jersey’s Board of Public Utilities Energy Master Plan Stakeholder Meetings 1&2
Apply for a 2020 Smart Growth Award!

07/16/2019

Apply for a 2020 Smart Growth Award!
2020 Redevelopment Forum: Save the date and submit suggestions

07/16/2019

2020 Redevelopment Forum: Save the date and submit suggestions
New Jersey Future is speaking at an Energy Master Plan stakeholder meeting (and you can, too!)

07/16/2019

New Jersey Future is speaking at an Energy Master Plan stakeholder meeting (and you can, too!)
Solutions Forum on Combined Sewage Overflows

07/10/2019

Solutions Forum on Combined Sewage Overflows
WEBINAR: Storm Water Compliance Success – Using Proactive BMPs To Minimize Regulatory Discharges

07/03/2019

WEBINAR: Storm Water Compliance Success – Using Proactive BMPs To Minimize Regulatory Discharges
Proposed stormwater rule change means green infrastructure training for municipal engineers

06/24/2019

Proposed stormwater rule change means green infrastructure training for municipal engineers
NJDOT Commitment to Communities Forum & Expo

06/21/2019

NJDOT Commitment to Communities Forum & Expo
7th Annual Coalition for the Delaware River Watershed Forum

06/21/2019

7th Annual Coalition for the Delaware River Watershed Forum
Perth Amboy Sewer Solutions Forum

06/10/2019

Perth Amboy Sewer Solutions Forum
WEBINAR: Designing Solar Land Use Laws that Protect Productive Farmland

06/10/2019

WEBINAR: Designing Solar Land Use Laws that Protect Productive Farmland
WEBINAR: How Utilities Are Addressing Water Equity

06/07/2019

WEBINAR: How Utilities Are Addressing Water Equity
WEBINAR: Affordable In-Law Suites and Backyard Bungalows – Capturing Opportunities in Accessory Dwelling Units

06/07/2019

WEBINAR: Affordable In-Law Suites and Backyard Bungalows – Capturing Opportunities in Accessory Dwelling Units
Jersey Water Works 2019 Membership Meeting

06/07/2019

Jersey Water Works 2019 Membership Meeting
Population Growth in Older Centers (but not all of them) Continues To Outstrip the Rest of the State

06/03/2019

Population Growth in Older Centers (but not all of them) Continues To Outstrip the Rest of the State
WEBINAR: Unlocking Opportunity Zones for Equitable Outcomes

06/03/2019

WEBINAR: Unlocking Opportunity Zones for Equitable Outcomes
Celebrating Women in Green

06/03/2019

Celebrating Women in Green
WEBINAR: How Technology can Improve Urban Design Engagement

06/03/2019

WEBINAR: How Technology can Improve Urban Design Engagement
Green Infrastructure & Stormwater Utilities Symposium

05/23/2019

Green Infrastructure & Stormwater Utilities Symposium
Downtown New Jersey’s 2019 Conference & Downtown Excellence Awards

05/22/2019

Downtown New Jersey’s 2019 Conference & Downtown Excellence Awards
Focus on Water for Infrastructure Week

05/21/2019

Focus on Water for Infrastructure Week
Newark’s Call to Collaboration

05/20/2019

Newark’s Call to Collaboration
Making TOD Real: Planning & Building Transit-Oriented Development in NJ

05/20/2019

Making TOD Real: Planning & Building Transit-Oriented Development in NJ
WEBINAR: NJ Land Use + Transit Data Application (NJLUTRANS.org)

05/20/2019

WEBINAR: NJ Land Use + Transit Data Application (NJLUTRANS.org)
WEBINAR: One Water in the States

05/17/2019

WEBINAR: One Water in the States
Stormwater Utilities Symposium

05/17/2019

Stormwater Utilities Symposium
New Jersey Complete Streets Summit

05/13/2019

New Jersey Complete Streets Summit
NJ Bicycle and Pedestrian Advisory Council (NJ BPAC) meeting

05/13/2019

NJ Bicycle and Pedestrian Advisory Council (NJ BPAC) meeting
ArtsTank Creative Placemaking Conference

05/10/2019

ArtsTank Creative Placemaking Conference
Green Infrastructure Tour & Picnic with RU Cooperative Extension

05/08/2019

Green Infrastructure Tour & Picnic with RU Cooperative Extension
Climate Resilient Municipalities: Controlling Stormwater, Protecting Streams & Maintaining Water Quality

05/08/2019

Climate Resilient Municipalities: Controlling Stormwater, Protecting Streams & Maintaining Water Quality
Transit Hub Guidebook Workshop

05/08/2019

Transit Hub Guidebook Workshop
Downtown Management Roundtable

05/08/2019

Downtown Management Roundtable
Job Growth Finally Following Population to Compact Centers

05/03/2019

Job Growth Finally Following Population to Compact Centers
Community Solar Pilot Program Now Accepting Applications

05/03/2019

Community Solar Pilot Program Now Accepting Applications
19th Annual Current Issues in Planning and Zoning Conference

04/29/2019

19th Annual Current Issues in Planning and Zoning Conference
2019 Excellence in GSI Awards Ceremony

04/29/2019

2019 Excellence in GSI Awards Ceremony
Are Millennials Leaving New Jersey Because Housing Costs Too Much?

04/22/2019

Are Millennials Leaving New Jersey Because Housing Costs Too Much?
WEBINAR – Geodesign: Using Data Transparency and Community Voices for Enhanced Land-Use Planning

04/22/2019

WEBINAR – Geodesign: Using Data Transparency and Community Voices for Enhanced Land-Use Planning
Earth Day Workshop at Kearny Point

04/19/2019

Earth Day Workshop at Kearny Point
Green Infrastructure Municipal Workshop

04/17/2019

Green Infrastructure Municipal Workshop
Waterfront Edge Design Guidelines (WEDG) 101

04/17/2019

Waterfront Edge Design Guidelines (WEDG) 101
New Jersey Future Executive Director To Co-Chair Waterfront Alliance Coastal Resilience Task Force

04/10/2019

New Jersey Future Executive Director To Co-Chair Waterfront Alliance Coastal Resilience Task Force
At Convention, Builders Take Interest in Green Infrastructure

04/10/2019

At Convention, Builders Take Interest in Green Infrastructure
Building a Culture of Health in New Jersey

04/10/2019

Building a Culture of Health in New Jersey
Meet-and-Greet with Mayor Wilsusen, Mayor Francis, and Ron Smith

04/03/2019

Meet-and-Greet with Mayor Wilsusen, Mayor Francis, and Ron Smith
USGBC NJ 2019 Awards Gala: LEEDing the Way

04/03/2019

USGBC NJ 2019 Awards Gala: LEEDing the Way
EARTH DAY AFTER PARTY 2019 & The Sustainable Trifecta

04/03/2019

EARTH DAY AFTER PARTY 2019 & The Sustainable Trifecta
Creative Urban Design

03/29/2019

Creative Urban Design
Crowdmapping

03/29/2019

Crowdmapping
Creating Community Murals

03/29/2019

Creating Community Murals
Creating Public Art

03/29/2019

Creating Public Art
WEBINAR: Incorporating arts in urban and site design

03/29/2019

WEBINAR: Incorporating arts in urban and site design
WEBINAR: How creative placemaking can help build more resilient communities

03/29/2019

WEBINAR: How creative placemaking can help build more resilient communities
WEBINAR: Cultural districts and cultural institutions: suns or black holes?

03/29/2019

WEBINAR: Cultural districts and cultural institutions: suns or black holes?
City of Water Day 2019

03/29/2019

City of Water Day 2019
MEETING: NY & NJ Harbor & Tributaries Focus Area Feasibility Study

03/29/2019

MEETING: NY & NJ Harbor & Tributaries Focus Area Feasibility Study
Main Street New Jersey Regional Workshop – Vineland

03/22/2019

Main Street New Jersey Regional Workshop – Vineland
Main Street New Jersey Regional Workshop – Montclair

03/22/2019

Main Street New Jersey Regional Workshop – Montclair
New Jersey’s Gold Coast Summit

03/18/2019

New Jersey’s Gold Coast Summit
Our Ocean and Beaches: A Record of Success and New Challenges to Face

03/15/2019

Our Ocean and Beaches: A Record of Success and New Challenges to Face
Governor’s Conference on Housing and Economic Development

03/15/2019

Governor’s Conference on Housing and Economic Development
Sustainability Summit & 10th Anniversary Celebration

03/04/2019

Sustainability Summit & 10th Anniversary Celebration
Meet-and-Greet with Evesham Mayor Jaclyn Veasy

03/01/2019

Meet-and-Greet with Evesham Mayor Jaclyn Veasy
Gateway Project Updates

03/01/2019

Gateway Project Updates
Progress 2019: New Jersey on the National Stage

03/01/2019

Progress 2019: New Jersey on the National Stage
2019 RPA Assembly

03/01/2019

2019 RPA Assembly
New Jersey Future Sends Letter to Governor Urging Him To Sign Stormwater Utility Legislation

02/27/2019

New Jersey Future Sends Letter to Governor Urging Him To Sign Stormwater Utility Legislation
Planning Manager David Kutner To Retire

02/27/2019

Planning Manager David Kutner To Retire
Lake Management Training

02/25/2019

Lake Management Training
Green Stormwater Management

02/25/2019

Green Stormwater Management
Restoration Ecology

02/25/2019

Restoration Ecology
Fundamentals of NSR / PSD Permitting

02/25/2019

Fundamentals of NSR / PSD Permitting
Coastal Community Resilience: An Overview of Strategies, Tools, and Science

02/25/2019

Coastal Community Resilience: An Overview of Strategies, Tools, and Science
Mid-Atlantic Greenways & Trails Summit

02/25/2019

Mid-Atlantic Greenways & Trails Summit
Northwest New Jersey Rivers Conference

02/18/2019

Northwest New Jersey Rivers Conference
Open Meeting: Our Water, Our Parks, Our Climate: Three Local Initiatives

02/18/2019

Open Meeting: Our Water, Our Parks, Our Climate: Three Local Initiatives
WEBINAR: Proactive Communication and Conflict Resolution for Redevelopment

02/18/2019

WEBINAR: Proactive Communication and Conflict Resolution for Redevelopment
eTOD Session: Community Ownership of Affordable Housing

02/18/2019

eTOD Session: Community Ownership of Affordable Housing
WEBINAR: Strategies to Promote Aging-Friendly Communities – The Land-Use Link

02/06/2019

WEBINAR: Strategies to Promote Aging-Friendly Communities – The Land-Use Link
New Jersey Future Submits Comments on Proposed Stormwater Rule Amendments

02/04/2019

New Jersey Future Submits Comments on Proposed Stormwater Rule Amendments
Infrastructure Week

02/04/2019

Infrastructure Week
Group of Mayors, Organizations Sends Letter Urging Gov. Murphy To Renew Focus on State Plan

02/01/2019

Group of Mayors, Organizations Sends Letter Urging Gov. Murphy To Renew Focus on State Plan
WEBINAR: Best Practices in Solar Planning and Zoning

02/01/2019

WEBINAR: Best Practices in Solar Planning and Zoning
New Jersey Future Statement on Passage of the Clean Stormwater, Flood Reduction Act

01/31/2019

New Jersey Future Statement on Passage of the Clean Stormwater, Flood Reduction Act
New Jersey Repositioning Summit

01/30/2019

New Jersey Repositioning Summit
New Jersey Economic Development Authority Announces $250,000 in Funding for Redeveloping Stranded Assets

01/29/2019

New Jersey Economic Development Authority Announces $250,000 in Funding for Redeveloping Stranded Assets
30th Annual Pinelands Short Course

01/28/2019

30th Annual Pinelands Short Course
NJ Spotlight – Improving New Jersey’s School Water Infrastructure

01/28/2019

NJ Spotlight – Improving New Jersey’s School Water Infrastructure
WEBINAR: Stormwater Utilities

01/28/2019

WEBINAR: Stormwater Utilities
BCONE Northeast Sustainable Communities Workshop 2019

01/25/2019

BCONE Northeast Sustainable Communities Workshop 2019
NJ TransAction 2019

01/25/2019

NJ TransAction 2019
AEA Spring Utility Management Conference

01/25/2019

AEA Spring Utility Management Conference
New Jersey Becoming Less Dangerous for Pedestrians, but Still Work To Do

01/23/2019

New Jersey Becoming Less Dangerous for Pedestrians, but Still Work To Do
Maintaining Green Infrastructure Practices/Projects

01/18/2019

Maintaining Green Infrastructure Practices/Projects
Moving from Planning to Implementation of Green Infrastructure

01/18/2019

Moving from Planning to Implementation of Green Infrastructure
How to Identify Green Infrastructure Projects in Your Town

01/18/2019

How to Identify Green Infrastructure Projects in Your Town
Main Street Now Conference

01/18/2019

Main Street Now Conference
The Future of Work

01/16/2019

The Future of Work
New Jersey Future Welcomes Three New Trustees

01/10/2019

New Jersey Future Welcomes Three New Trustees
Imagine a Day Without Water

01/10/2019

Imagine a Day Without Water
Solving US and Global Water Inequities: Sharing Solutions from Around the World

01/10/2019

Solving US and Global Water Inequities: Sharing Solutions from Around the World
Report Gives New Jersey High Marks for Designating Opportunity Zones in Smart-Growth Locations

01/09/2019

Report Gives New Jersey High Marks for Designating Opportunity Zones in Smart-Growth Locations
WEBINAR: Certificate in Creative Placemaking

01/07/2019

WEBINAR: Certificate in Creative Placemaking
2019 Atlantic Builders Convention

01/04/2019

2019 Atlantic Builders Convention
TNJ Institute: Green Infrastructure and Transportation

01/04/2019

TNJ Institute: Green Infrastructure and Transportation
Together North Jersey Forum and Task Force Meetings

01/04/2019

Together North Jersey Forum and Task Force Meetings
Creating a Great Shuttle Service

01/04/2019

Creating a Great Shuttle Service
WEBINAR: Utility Strengthening Through Consolidation

01/04/2019

WEBINAR: Utility Strengthening Through Consolidation
DEP Moves to Require Green Infrastructure for Stormwater Management

12/06/2018

DEP Moves to Require Green Infrastructure for Stormwater Management
EPA Announces $56 Million in Brownfields Grants for 2019

12/03/2018

EPA Announces $56 Million in Brownfields Grants for 2019
Where Do New Jersey’s Out-Migrating Millennials Go?

11/07/2018

Where Do New Jersey’s Out-Migrating Millennials Go?
From Stormwater to Clean Water: New Flood-Control, Pollution Resource for Towns

11/05/2018

From Stormwater to Clean Water: New Flood-Control, Pollution Resource for Towns
A Better Way To Plan for Traffic Effects of New Development

11/02/2018

A Better Way To Plan for Traffic Effects of New Development
Where Do New Jersey’s Out-Migrants Go?

10/25/2018

Where Do New Jersey’s Out-Migrants Go?
New Jersey Future Releases Action Plan for Trenton Transit Center Area

10/23/2018

New Jersey Future Releases Action Plan for Trenton Transit Center Area
DEP Gathers Input at Coastal Resilience Summit on Local Actions To Plan for Climate Change

10/23/2018

DEP Gathers Input at Coastal Resilience Summit on Local Actions To Plan for Climate Change
New Jersey Future Contributes Resiliency Planning Chapter to Planning Guide

10/12/2018

New Jersey Future Contributes Resiliency Planning Chapter to Planning Guide
The Transportation-Emissions Reduction Strategy No One’s Talking About

10/08/2018

The Transportation-Emissions Reduction Strategy No One’s Talking About
New Jersey Future To Participate in Trenton Innovation Challenge Grant

10/02/2018

New Jersey Future To Participate in Trenton Innovation Challenge Grant
Stormwater Camp: A Summer Week To Remember

09/25/2018

Stormwater Camp: A Summer Week To Remember
New Model Ordinance Will Help Reduce Polluted Runoff in New Jersey

09/04/2018

New Model Ordinance Will Help Reduce Polluted Runoff in New Jersey
DOT’s Municipal Aid: Look Beneath the (Re)Surface for Innovative Uses

08/17/2018

DOT’s Municipal Aid: Look Beneath the (Re)Surface for Innovative Uses
DOT’s Municipal Aid: Look Beneath the (Re)Surface for Innovative Uses

08/17/2018

DOT’s Municipal Aid: Look Beneath the (Re)Surface for Innovative Uses
Are the Suburbs Back? Depends On How You Define ‘Suburb’

08/13/2018

Are the Suburbs Back? Depends On How You Define ‘Suburb’
Combined Sewer Permit Holders Meet Report Deadline

07/25/2018

Combined Sewer Permit Holders Meet Report Deadline
Eleven Great One Water Ideas From the Jersey Water Works Membership Meeting

07/24/2018

Eleven Great One Water Ideas From the Jersey Water Works Membership Meeting
DOT Offers Help in Applying for Federal Transportation Grants

05/31/2018

DOT Offers Help in Applying for Federal Transportation Grants
The March Toward Walkable Urbanism Continues

05/25/2018

The March Toward Walkable Urbanism Continues
Green Infrastructure Draws Attention at Atlantic Builders Convention

05/16/2018

Green Infrastructure Draws Attention at Atlantic Builders Convention
One Water Awards Nominations Open, Partnership Expands

05/03/2018

One Water Awards Nominations Open, Partnership Expands
Exploring Green Infrastructure Options for Your Project? These Tools Can Help.

05/01/2018

Exploring Green Infrastructure Options for Your Project? These Tools Can Help.
New Jersey Future Resources Highlighted at National Planners Convention

05/01/2018

New Jersey Future Resources Highlighted at National Planners Convention
Water Infrastructure a Major Topic at Budget Hearing for DEP

04/26/2018

Water Infrastructure a Major Topic at Budget Hearing for DEP
Bayonne Water Guardians, Kearny AWAKE and Harrison TIDE Champion Green Initiatives

04/18/2018

Bayonne Water Guardians, Kearny AWAKE and Harrison TIDE Champion Green Initiatives
Opportunity Zones Take Another Step Forward

04/10/2018

Opportunity Zones Take Another Step Forward
How Do We Pay for New Jersey’s Aging Stormwater Infrastructure?

04/04/2018

How Do We Pay for New Jersey’s Aging Stormwater Infrastructure?
A Competition Over Placemaking

04/02/2018

A Competition Over Placemaking
Maximizing the Impact of Public-Private Partnerships

03/30/2018

Maximizing the Impact of Public-Private Partnerships
Making New Jersey’s Communities More Aging-Friendly

03/29/2018

Making New Jersey’s Communities More Aging-Friendly
Trends in Redevelopment Finance: Complexity and Change

03/27/2018

Trends in Redevelopment Finance: Complexity and Change
County Population Estimates: Return to the Urban Core Continues

03/26/2018

County Population Estimates: Return to the Urban Core Continues
Millennials: What Do They Want?

03/20/2018

Millennials: What Do They Want?
The New Leadership Is Local

03/16/2018

The New Leadership Is Local
Workshop Highlights the Benefits of Green Infrastructure to Developers

02/06/2018

Workshop Highlights the Benefits of Green Infrastructure to Developers
Remembering Brendan Byrne

01/05/2018

Remembering Brendan Byrne
Drinking Water Infrastructure Report Calls for Investment, Transparency

01/04/2018

Drinking Water Infrastructure Report Calls for Investment, Transparency
Bill Would Cap Sewerage Authorities Ability To Raise Funds for System Repairs

01/04/2018

Bill Would Cap Sewerage Authorities Ability To Raise Funds for System Repairs
Getting Sewage Off Our Streets and Out of Our Rivers

12/18/2018

Getting Sewage Off Our Streets and Out of Our Rivers
Yes, Millennials Really Are Fleeing the State. The Data Say So.

09/12/2018

Yes, Millennials Really Are Fleeing the State. The Data Say So.
New Report Highlights Green Infrastructure Financing Opportunities

07/19/2018

New Report Highlights Green Infrastructure Financing Opportunities
Survey: New Jersey Residents Name Clean Drinking Water as Top Environmental Priority

03/28/2018

Survey: New Jersey Residents Name Clean Drinking Water as Top Environmental Priority
New Jersey Shows Small Population Growth in Latest Census Estimate

12/20/2017

New Jersey Shows Small Population Growth in Latest Census Estimate
How the Fourth Regional Plan Could Affect New Jersey

12/12/2017

How the Fourth Regional Plan Could Affect New Jersey
Water Conference Urges Action From New Jersey’s New Administration

12/06/2017

Water Conference Urges Action From New Jersey’s New Administration
A Year One Clean Water Agenda for the New Governor

11/30/2017

A Year One Clean Water Agenda for the New Governor
Smart-Growth Policy Priorities Well Represented on Murphy Transition Team

11/27/2017

Smart-Growth Policy Priorities Well Represented on Murphy Transition Team
A Rain Garden Grows in Harrison

11/22/2017

A Rain Garden Grows in Harrison
What New Jersey Can Learn From Washington, D.C., About Transportation Improvements

11/17/2017

What New Jersey Can Learn From Washington, D.C., About Transportation Improvements
Rain Garden Partnership in Newton Brings Learning Opportunity, Better Water Quality

11/03/2017

Rain Garden Partnership in Newton Brings Learning Opportunity, Better Water Quality
New Report Shows New Jersey Is Still on the ‘Long Road Home’ After Sandy

10/25/2017

New Report Shows New Jersey Is Still on the ‘Long Road Home’ After Sandy
Symposium Addresses Dangers of Inaction on Climate Change

10/18/2017

Symposium Addresses Dangers of Inaction on Climate Change
Analysis: New Jersey Is Losing Its Millennials

09/28/2017

Analysis: New Jersey Is Losing Its Millennials
Newark Philadelphia Study Visit Focuses on Implementing Green Infrastructure at Scale

09/27/2017

Newark Philadelphia Study Visit Focuses on Implementing Green Infrastructure at Scale
Gubernatorial Candidates on Key Issues Facing New Jersey

09/19/2017

Gubernatorial Candidates on Key Issues Facing New Jersey
Proposed Rule Change Would Allow Development on Piers

09/18/2017

Proposed Rule Change Would Allow Development on Piers
Lead in Drinking Water Results Ready for “Back to School” Season

08/31/2017

Lead in Drinking Water Results Ready for “Back to School” Season
Lead in Drinking Water Results Ready for ‘Back to School’ Season

08/31/2017

Lead in Drinking Water Results Ready for ‘Back to School’ Season
Joint Environment Committee Dives in on Climate Change, Coastal Resilience

08/14/2017

Joint Environment Committee Dives in on Climate Change, Coastal Resilience
Good News, Bad News in New Monmouth Poll

08/02/2017

Good News, Bad News in New Monmouth Poll
Sound Management, Transparency Key to Ensuring Reliable, Reasonably Priced Drinking Water

07/24/2017

Sound Management, Transparency Key to Ensuring Reliable, Reasonably Priced Drinking Water
McKinsey’s Smart Economic Vision for New Jersey

07/20/2017

McKinsey’s Smart Economic Vision for New Jersey
New Jersey Future Testifies at U.S. Senate Roundtable on Lead in Drinking Water

07/14/2017

New Jersey Future Testifies at U.S. Senate Roundtable on Lead in Drinking Water
Images Available for Educational Signage on Combined-Sewer Outfalls

06/29/2017

Images Available for Educational Signage on Combined-Sewer Outfalls
Many States Making New Investments in Water Infrastructure

06/28/2017

Many States Making New Investments in Water Infrastructure
Jersey Water Works Co-Sponsors New One Water Awards Program

06/12/2017

Jersey Water Works Co-Sponsors New One Water Awards Program
Census Numbers Confirm Renewed Growth in Urban Areas

05/26/2017

Census Numbers Confirm Renewed Growth in Urban Areas
Report: Changes in Affordable Housing Tax Credit Criteria Move More People to High-Opportunity Areas

05/23/2017

Report: Changes in Affordable Housing Tax Credit Criteria Move More People to High-Opportunity Areas
“Re-Forum” Will Tackle Updates to State’s Land-Use Law

05/05/2017

“Re-Forum” Will Tackle Updates to State’s Land-Use Law
New Office Market Report: Transit Service Is Key

04/12/2017

New Office Market Report: Transit Service Is Key
What is the Value of Green Infrastructure? New Tools and Events Drill Down

04/11/2017

What is the Value of Green Infrastructure? New Tools and Events Drill Down
Forum Roundup: Reinforce Your Redevelopment Strategy With Good Data

04/10/2017

Forum Roundup: Reinforce Your Redevelopment Strategy With Good Data
Forum Roundup: Making the Affordable Housing Numbers Work(able)

04/05/2017

Forum Roundup: Making the Affordable Housing Numbers Work(able)
Forum Roundup: Reimagining the Suburbs

03/27/2017

Forum Roundup: Reimagining the Suburbs
Guide Helps Unlock New Resources for Stormwater Management

03/23/2017

Guide Helps Unlock New Resources for Stormwater Management
Forum Feature: Federal Redevelopment Tools: Existential Threats, and a Few Opportunities

03/20/2017

Forum Feature: Federal Redevelopment Tools: Existential Threats, and a Few Opportunities
Forum Roundtable: Getting to a Regional Approach to Coastal Resilience

03/20/2017

Forum Roundtable: Getting to a Regional Approach to Coastal Resilience
Forum Roundup: The Changing Downtown Retail Paradigm

03/20/2017

Forum Roundup: The Changing Downtown Retail Paradigm
Forum Roundup: The Future of Parking: Less Parking, Better Management

03/17/2017

Forum Roundup: The Future of Parking: Less Parking, Better Management
Recommendations for the Next Governor

03/10/2017

Recommendations for the Next Governor
Planning for Sea-Level Rise VII: Disclosure

02/21/2017

Planning for Sea-Level Rise VII: Disclosure
Planning for Sea-Level Rise VI: Tax Districts

02/17/2017

Planning for Sea-Level Rise VI: Tax Districts
Planning for Sea-Level Rise V: Overlay Zones

02/16/2017

Planning for Sea-Level Rise V: Overlay Zones
Planning for Sea-Level Rise IV: Changes to Building and Site Standards

02/08/2017

Planning for Sea-Level Rise IV: Changes to Building and Site Standards
Planning for Sea-Level Rise III: Restricting Development

02/08/2017

Planning for Sea-Level Rise III: Restricting Development
Remembering Caren Franzini

01/26/2017

Remembering Caren Franzini
Developers Convention To Address ‘Why Green Infrastructure?’

01/24/2017

Developers Convention To Address ‘Why Green Infrastructure?’
To Speak at Planning Conference

01/19/2017

To Speak at Planning Conference
New Jersey Future Staff To Speak at Planning Conference

01/19/2017

New Jersey Future Staff To Speak at Planning Conference
Planning for Sea-Level Rise II: Redirecting Development

01/10/2017

Planning for Sea-Level Rise II: Redirecting Development
Planning for Sea-Level Rise I: Accounting for Damage

01/10/2017

Planning for Sea-Level Rise I: Accounting for Damage
New Report Outlines Coastal Resilience Strategies

12/13/2017

New Report Outlines Coastal Resilience Strategies
Remembering Al Koeppe

12/06/2016

Remembering Al Koeppe
New Reports Assess State’s Exposure to Sea-Level Rise

11/18/2016

New Reports Assess State’s Exposure to Sea-Level Rise
New Jersey Future Hosts National Gathering

11/16/2016

New Jersey Future Hosts National Gathering
Art in the Capital City

11/14/2016

Art in the Capital City
New Reports Assess State’s Exposure to Sea-Level Rise

11/08/2016

New Reports Assess State’s Exposure to Sea-Level Rise
Population Trends at the Jersey Shore, Part 2: The Sandy Effect

11/01/2016

Population Trends at the Jersey Shore, Part 2: The Sandy Effect
Documentary Featuring Sea Bright, New Jersey Future Is Ocean Film Festival Finalist

10/20/2016

Documentary Featuring Sea Bright, New Jersey Future Is Ocean Film Festival Finalist
Population Trends at the Jersey Shore, Part 1: Long-Term

10/17/2016

Population Trends at the Jersey Shore, Part 1: Long-Term
New Jersey Recovery Fund Shares Post-Sandy Resiliency Lessons With Chinese Delegation

10/12/2016

New Jersey Recovery Fund Shares Post-Sandy Resiliency Lessons With Chinese Delegation
What Can 23 Cents Buy?

10/05/2016

What Can 23 Cents Buy?
NJ Spotlight on Cities Looks Toward an Urban Agenda for New Jersey

09/28/2016

NJ Spotlight on Cities Looks Toward an Urban Agenda for New Jersey
Explainer: How to Think About New Jersey’s Population (and Income) Growth

09/14/2016

Explainer: How to Think About New Jersey’s Population (and Income) Growth
School District Regionalization: The Land-Use Connection

08/22/2016

School District Regionalization: The Land-Use Connection
Lead Found in School Drinking Water Across New Jersey

08/10/2016

Lead Found in School Drinking Water Across New Jersey
Jersey Water Works Membership Meeting: Collaboration Is the Key

07/28/2016

Jersey Water Works Membership Meeting: Collaboration Is the Key
Three Communities Step Up To Mainstream Green Infrastructure

07/27/2016

Three Communities Step Up To Mainstream Green Infrastructure
New Jersey Future Trustee Receives NJUA Distinguished Service Award

07/13/2016

New Jersey Future Trustee Receives NJUA Distinguished Service Award
Design Professionals Walk Away With Practical Green Infrastructure Insights

06/24/2016

Design Professionals Walk Away With Practical Green Infrastructure Insights
New Jersey Future Wins National Award for Sandy Report

06/23/2016

New Jersey Future Wins National Award for Sandy Report
New Jersey Future’s Teri Jover Named Sustainability Hero

06/02/2016

New Jersey Future’s Teri Jover Named Sustainability Hero
New Jersey Future’s Teri Jover Named Sustainability Hero

06/02/2016

New Jersey Future’s Teri Jover Named Sustainability Hero
Jersey Water Works Delegation To Attend National Water Conference

05/26/2016

Jersey Water Works Delegation To Attend National Water Conference
Three New Jersey Cities Selected To Accelerate Water Infrastructure Innovation

05/25/2016

Three New Jersey Cities Selected To Accelerate Water Infrastructure Innovation
Smart Growth Award-Winner Wesmont Station Opens

05/23/2016

Smart Growth Award-Winner Wesmont Station Opens
Built-Out Places Account for Majority of State’s Population Growth Since 2008

05/20/2016

Built-Out Places Account for Majority of State’s Population Growth Since 2008
Built-Out Places Account for Majority of State’s Population Growth Since 2008

05/20/2016

Built-Out Places Account for Majority of State’s Population Growth Since 2008
Forum Roundup: Green Bonds: Financing our Future

05/18/2016

Forum Roundup: Green Bonds: Financing our Future
Leaders From 34 Municipalities Learn About Green Infrastructure

05/17/2016

Leaders From 34 Municipalities Learn About Green Infrastructure
Infrastructure Matters

05/16/2016

Infrastructure Matters
Fifteen Years of Smart Growth Success

05/13/2016

Fifteen Years of Smart Growth Success
Chuck Marohn on the Value of Roads, Streets, and People

05/04/2016

Chuck Marohn on the Value of Roads, Streets, and People
Jersey Water Works Releases 2016 Workplan

04/27/2016

Jersey Water Works Releases 2016 Workplan
Forum Roundup: The Triple-Bottom-Line Beauty of Green Infrastructure

04/19/2016

Forum Roundup: The Triple-Bottom-Line Beauty of Green Infrastructure
Demand for Transit Neighborhoods on the Rise

04/18/2016

Demand for Transit Neighborhoods on the Rise
Case Study: How Bioswales Are Helping To Clean Brooklyn’s Gowanus Canal

04/11/2016

Case Study: How Bioswales Are Helping To Clean Brooklyn’s Gowanus Canal
Forum Feature: We Need To Do Transportation Planning for People, Not Cars. And We Need To Do It Fast.

04/06/2016

Forum Feature: We Need To Do Transportation Planning for People, Not Cars. And We Need To Do It Fast.
Forum Roundup: Gateway Tunnel Will Provide Much-Needed New Transit Capacity

04/04/2016

Forum Roundup: Gateway Tunnel Will Provide Much-Needed New Transit Capacity
The Greatest Danger Facing New Jersey’s Water Infrastructure: The Unknown

04/04/2016

The Greatest Danger Facing New Jersey’s Water Infrastructure: The Unknown
Forum Roundup: The Mega-Ships Are Here! Are We Ready?

03/28/2016

Forum Roundup: The Mega-Ships Are Here! Are We Ready?
Public-Interest Organizations Urge Commitment of Disaster Competition Award Funds to Regional Planning

03/24/2016

Public-Interest Organizations Urge Commitment of Disaster Competition Award Funds to Regional Planning
Forum Roundup: Finding the Opportunities in Affordable Housing

03/23/2016

Forum Roundup: Finding the Opportunities in Affordable Housing
Forum Roundup: Cities, Redevelopers Join Forces To Tackle Floodproofing, Sewer Upgrades

03/22/2016

Forum Roundup: Cities, Redevelopers Join Forces To Tackle Floodproofing, Sewer Upgrades
New Jersey’s Population Is Still Growing

03/17/2016

New Jersey’s Population Is Still Growing
New Jersey’s Population Is Still Growing

03/17/2016

New Jersey’s Population Is Still Growing
Design Competition Aims To Accelerate Water Infrastructure Innovation

03/15/2016

Design Competition Aims To Accelerate Water Infrastructure Innovation
Happy Birthday, New Jersey State Plan!

03/07/2016

Happy Birthday, New Jersey State Plan!
New Initiative Is Working To Mainstream Green Infrastructure

02/23/2016

New Initiative Is Working To Mainstream Green Infrastructure
Would Buyouts Be Good for Flood-Prone Mystic Island?

02/18/2016

Would Buyouts Be Good for Flood-Prone Mystic Island?
Green Infrastructure Taking Off in Paterson

02/18/2016

Green Infrastructure Taking Off in Paterson
New Zoning Codes: More Housing Options, More Mixed Use, Less Parking

02/09/2016

New Zoning Codes: More Housing Options, More Mixed Use, Less Parking
Flint’s Wake-Up Call for New Jersey — and the Nation

02/05/2016

Flint’s Wake-Up Call for New Jersey — and the Nation
Bayside Flooding Highlights Inherent Vulnerability of Barrier Islands

01/27/2016

Bayside Flooding Highlights Inherent Vulnerability of Barrier Islands
Overcoming Developer Obstacles to Redevelopment

01/26/2016

Overcoming Developer Obstacles to Redevelopment
Fixing Flooding in Communities Through Collaboration

01/22/2016

Fixing Flooding in Communities Through Collaboration
New Jersey Future Trustee Inducted Into Business Hall of Fame

01/19/2016

New Jersey Future Trustee Inducted Into Business Hall of Fame
Smart Growth in the Somerset Hills

01/13/2016

Smart Growth in the Somerset Hills
Sewage Overflow Warning Signs Popping Up

01/07/2016

Sewage Overflow Warning Signs Popping Up
Conference Pinpoints Water as Defining Issue for Next Generation

12/15/2015

Conference Pinpoints Water as Defining Issue for Next Generation
Introducing Jersey Water Works!

12/15/2015

Introducing Jersey Water Works!
Workshop Focuses on Helping Coastal Communities Confront Climate Risks

12/15/2015

Workshop Focuses on Helping Coastal Communities Confront Climate Risks
Can New Jersey’s Older Residents Afford Their Housing?

12/08/2015

Can New Jersey’s Older Residents Afford Their Housing?
New Jersey Gets a D+ on New Climate Preparedness Report Card

11/19/2015

New Jersey Gets a D+ on New Climate Preparedness Report Card
Report: Fiscal Implications of Development Patterns on Road Usage

11/10/2015

Report: Fiscal Implications of Development Patterns on Road Usage
New Jersey Future Celebrates George Pruitt

11/03/2015

New Jersey Future Celebrates George Pruitt
Rebuild By Design Resiliency Projects: A Status Update

10/28/2015

Rebuild By Design Resiliency Projects: A Status Update
Are Towns in a Better Position to Make Long-Term Resiliency Decisions?

10/27/2015

Are Towns in a Better Position to Make Long-Term Resiliency Decisions?
NJ Spotlight on Cities: Successful Development Requires a Community’s Blessing

10/26/2015

NJ Spotlight on Cities: Successful Development Requires a Community’s Blessing
New Driver for Downtown Economic Development in Trenton

10/19/2015

New Driver for Downtown Economic Development in Trenton
Research Reveals Recession’s Leveling Effect on Residential Development

10/06/2015

Research Reveals Recession’s Leveling Effect on Residential Development
Post-Recession, Housing Growth and Value in Distressed Municipalities Keep Pace With Non-Distressed

10/05/2015

Post-Recession, Housing Growth and Value in Distressed Municipalities Keep Pace With Non-Distressed
Housing and Community Development Network Honors New Jersey Future With Community Partner Award

09/24/2015

Housing and Community Development Network Honors New Jersey Future With Community Partner Award
Surgeon General’s #StepItUp Campaign Highlights Land-Use Challenges to Regular Walking

09/10/2015

Surgeon General’s #StepItUp Campaign Highlights Land-Use Challenges to Regular Walking
New Jersey Future To Honor George Pruitt, Pioneer in Higher Education, Trenton Revitalization

09/01/2015

New Jersey Future To Honor George Pruitt, Pioneer in Higher Education, Trenton Revitalization
New Jersey Future Trustee Gilbert To Receive NJPO Lifetime Achievement Award

08/19/2015

New Jersey Future Trustee Gilbert To Receive NJPO Lifetime Achievement Award
Entering a New Era of New Jersey Urban Water Quality

08/14/2015

Entering a New Era of New Jersey Urban Water Quality
Transportation, Housing Improvements Needed To Make New Jersey Towns More Aging-Friendly

08/12/2015

Transportation, Housing Improvements Needed To Make New Jersey Towns More Aging-Friendly
Outreach Plan for Hoboken Rebuild By Design Project Needs Improvement

08/04/2015

Outreach Plan for Hoboken Rebuild By Design Project Needs Improvement
Can Somerset County Attract Millennials?

07/30/2015

Can Somerset County Attract Millennials?
New Jersey Future Board Chairman Named to Monmouth University’s First Endowed Chair in Real Estate Policy

07/27/2015

New Jersey Future Board Chairman Named to Monmouth University’s First Endowed Chair in Real Estate Policy
State Planning Commission Set To Extend Center Designations; Leaves Coastal Towns at Risk

07/10/2015

State Planning Commission Set To Extend Center Designations; Leaves Coastal Towns at Risk
Two New Transit Villages Named, Including Second Bus-Centered Designation

07/10/2015

Two New Transit Villages Named, Including Second Bus-Centered Designation
Making Our Coastline Both Resilient and Prosperous

07/08/2015

Making Our Coastline Both Resilient and Prosperous
Survey Will Gather Input on Health Effects of Flooding in Hoboken

07/01/2015

Survey Will Gather Input on Health Effects of Flooding in Hoboken
New Jersey Moves to Final Round in National Disaster Resiliency Competition

06/29/2015

New Jersey Moves to Final Round in National Disaster Resiliency Competition
New Study Shines a Light on Mixed-Income Housing Around New Jersey’s Transit Stations

06/22/2015

New Study Shines a Light on Mixed-Income Housing Around New Jersey’s Transit Stations
New Report Highlights National Trend: Corporations Are Investing Downtown

06/18/2015

New Report Highlights National Trend: Corporations Are Investing Downtown
Millennials, ‘Alternative’ Economy Shape Downtown Redevelopment Trends

06/15/2015

Millennials, ‘Alternative’ Economy Shape Downtown Redevelopment Trends
NJ Transit Fare Increase: An Unfair Approach to Transportation Funding

05/15/2015

NJ Transit Fare Increase: An Unfair Approach to Transportation Funding
The Public Wins a Strengthened Role in Rebuild By Design Projects

05/13/2015

The Public Wins a Strengthened Role in Rebuild By Design Projects
Incorporating Green Infrastructure: The Time Is Now

05/13/2015

Incorporating Green Infrastructure: The Time Is Now
New Jersey Future Welcomes New Trustees

05/05/2015

New Jersey Future Welcomes New Trustees
College Papers on Key New Jersey Policy Issues Win Statewide Academic Award

05/04/2015

College Papers on Key New Jersey Policy Issues Win Statewide Academic Award
Planning Our Coastal Future: Little Egg Harbor and Tuckerton

04/28/2015

Planning Our Coastal Future: Little Egg Harbor and Tuckerton
League of Municipalities Executive Director To Retire

04/28/2015

League of Municipalities Executive Director To Retire
Raising Awareness of our Urban Water Infrastructure on #UndertheEarthDay

04/22/2015

Raising Awareness of our Urban Water Infrastructure on #UndertheEarthDay
New Jersey Future Joins National Infrastructure Week With Free Webinar May 14

04/21/2015

New Jersey Future Joins National Infrastructure Week With Free Webinar May 14
New Meadowlands Project Under Way

04/13/2015

New Meadowlands Project Under Way
Community Meetings To Focus on Flood Vulnerability, Potential Solutions

04/10/2015

Community Meetings To Focus on Flood Vulnerability, Potential Solutions
Forum Plenary: Impact Investing and Systems Thinking

04/10/2015

Forum Plenary: Impact Investing and Systems Thinking
2015 Smart Growth Award Winners Announced

03/30/2015

2015 Smart Growth Award Winners Announced
Opinion: Bill To Reform Meadowlands Commission an Ill-Planned Clean-Up Attempt

03/26/2015

Opinion: Bill To Reform Meadowlands Commission an Ill-Planned Clean-Up Attempt
Meadowlands ‘Cleanup Bill’ Needs Cleaning Up

03/18/2015

Meadowlands ‘Cleanup Bill’ Needs Cleaning Up
Forum Keynote: Opportunities (and Challenges) for Great Change

03/18/2015

Forum Keynote: Opportunities (and Challenges) for Great Change
Release of Combined-Sewer Permits Should Trigger Generational Investments in Affected Communities

03/17/2015

Release of Combined-Sewer Permits Should Trigger Generational Investments in Affected Communities
State’s Application to National Disaster Resilience Competition Is Strong, Can Be Stronger

03/12/2015

State’s Application to National Disaster Resilience Competition Is Strong, Can Be Stronger
COAH Decision Will Allow New Jersey To Move Forward With Fair Housing Process

03/10/2015

COAH Decision Will Allow New Jersey To Move Forward With Fair Housing Process
New Jersey Enters National Disaster Resilience Contest

02/27/2015

New Jersey Enters National Disaster Resilience Contest
DEP Approves Permits To Restore Assunpink Creek

02/19/2015

DEP Approves Permits To Restore Assunpink Creek
New Jersey Future Trustee Ingrid Reed Wins AIA-NJ Award

02/18/2015

New Jersey Future Trustee Ingrid Reed Wins AIA-NJ Award
Experts Detail Challenges of Adapting to Climate Change

02/17/2015

Experts Detail Challenges of Adapting to Climate Change
New Jersey Future Vulnerability Assessment Process To Be Presented at National Conference

02/06/2015

New Jersey Future Vulnerability Assessment Process To Be Presented at National Conference
New Jersey Future, Other Groups Urge Veto of ‘Meadowlands Bill’

02/04/2015

New Jersey Future, Other Groups Urge Veto of ‘Meadowlands Bill’
White House Executive Order May Make Shore Communities Less Vulnerable to Storm Damage

02/02/2015

White House Executive Order May Make Shore Communities Less Vulnerable to Storm Damage
CNU President Is 2015 Forum Keynote Speaker

01/27/2015

CNU President Is 2015 Forum Keynote Speaker
Extending Approval for State Plan Centers Could Harm Coastal Towns

01/23/2015

Extending Approval for State Plan Centers Could Harm Coastal Towns
Rebuild By Design Projects Must Ensure Equity, Resiliency, Public Involvement

01/21/2015

Rebuild By Design Projects Must Ensure Equity, Resiliency, Public Involvement
Workshop Attendees Learn Innovative Approaches to Addressing Combined-Sewer Overflows

01/20/2015

Workshop Attendees Learn Innovative Approaches to Addressing Combined-Sewer Overflows
To Speak at APA-NJ Conference

01/15/2015

To Speak at APA-NJ Conference
Reinvesting in Urban Water Infrastructure through Combined Sewer Overflow Long Term Control Plans

01/15/2015

Reinvesting in Urban Water Infrastructure through Combined Sewer Overflow Long Term Control Plans
New Jersey Future Staff To Speak at APA-NJ Conference

01/15/2015

New Jersey Future Staff To Speak at APA-NJ Conference
Study Highlights Opportunities for Green Infrastructure in Trenton

01/06/2015

Study Highlights Opportunities for Green Infrastructure in Trenton
Plan Released for Third Round of Federal Sandy Funds

12/19/2014

Plan Released for Third Round of Federal Sandy Funds
New Jersey Lags Behind in Some Key Real Estate Trends

12/12/2014

New Jersey Lags Behind in Some Key Real Estate Trends
Opinion: We Can’t Afford the Price We Pay for Cheap Water

12/10/2014

Opinion: We Can’t Afford the Price We Pay for Cheap Water
Economic Opportunity Act Retains Incentives Focus on Smart-Growth Locations

12/05/2014

Economic Opportunity Act Retains Incentives Focus on Smart-Growth Locations
How Can We Discuss Climate Change Constructively?

12/02/2014

How Can We Discuss Climate Change Constructively?
Downtown Revitalization Survey Shows Need for Towns To Be More Proactive

11/19/2014

Downtown Revitalization Survey Shows Need for Towns To Be More Proactive
Fourth Regional Plan Conference Themes: Revitalization, Technology, Affordability and Access

11/17/2014

Fourth Regional Plan Conference Themes: Revitalization, Technology, Affordability and Access
Thought Leaders To Gather at Regional Conference

11/10/2014

Thought Leaders To Gather at Regional Conference
Clement A. Price

11/06/2014

Clement A. Price
Lincoln Institute Symposium: Collaboration, Regional Focus Are Keys to Successful Resilience

11/06/2014

Lincoln Institute Symposium: Collaboration, Regional Focus Are Keys to Successful Resilience
John Heldrich, a Civic Visionary

11/01/2014

John Heldrich, a Civic Visionary
Water Infrastructure Funds: An Opportunity To Make Communities More Resilient

10/22/2014

Water Infrastructure Funds: An Opportunity To Make Communities More Resilient
Community Meeting Brings Assunpink Daylighting to the Light of Day

10/21/2014

Community Meeting Brings Assunpink Daylighting to the Light of Day
Creating a Model for Statewide, Nationwide Innovation

10/16/2014

Creating a Model for Statewide, Nationwide Innovation
Innovative Initiatives Can Lead the Way

10/09/2014

Innovative Initiatives Can Lead the Way
Princeton Is First New Jersey Community To Earn WHO ‘Age-Friendly’ Designation

10/06/2014

Princeton Is First New Jersey Community To Earn WHO ‘Age-Friendly’ Designation
Princeton Is First New Jersey Community To Earn WHO ‘Age-Friendly’ Designation

10/06/2014

Princeton Is First New Jersey Community To Earn WHO ‘Age-Friendly’ Designation
Remembering John Sheridan

10/03/2014

Remembering John Sheridan
Time To Make Some Noise

10/02/2014

Time To Make Some Noise
New Jersey Future Partners With Lincoln Institute To Host Resiliency Symposium

09/30/2014

New Jersey Future Partners With Lincoln Institute To Host Resiliency Symposium
New Jersey Future To Honor Trustee Henry A. Coleman

09/23/2014

New Jersey Future To Honor Trustee Henry A. Coleman
ProWalk ProBike ProPlace: Making Active Transportation Happen

09/23/2014

ProWalk ProBike ProPlace: Making Active Transportation Happen
New Jersey Should Re-Join Greenhouse Gas Initiative

09/18/2014

New Jersey Should Re-Join Greenhouse Gas Initiative
Survey Will Help Identify Downtown Revitalization Needs

09/17/2014

Survey Will Help Identify Downtown Revitalization Needs
Stormwater Utilities: A Tool for Managing Rainwater Runoff

09/16/2014

Stormwater Utilities: A Tool for Managing Rainwater Runoff
Energy Resiliency Bank Proposal: Right Concept, but Needs Detail To Protect Against Flooding

09/15/2014

Energy Resiliency Bank Proposal: Right Concept, but Needs Detail To Protect Against Flooding
Sept. 15 Community Meeting Will Focus on Reopening of Downtown Trenton’s Assunpink Creek

09/11/2014

Sept. 15 Community Meeting Will Focus on Reopening of Downtown Trenton’s Assunpink Creek
Delegation From Japan Visits To Compare Notes on Disaster Preparedness

09/11/2014

Delegation From Japan Visits To Compare Notes on Disaster Preparedness
Report: Prompt Action Is Needed for Best-Practices Upgrade of New Jersey’s Urban Water Infrastructure

09/09/2014

Report: Prompt Action Is Needed for Best-Practices Upgrade of New Jersey’s Urban Water Infrastructure
Creating a Voice for the Voiceless in a Changing Urban Climate

09/04/2014

Creating a Voice for the Voiceless in a Changing Urban Climate
Documentary About Coastal Development in New Jersey To Be Shown in Rumson

08/27/2014

Documentary About Coastal Development in New Jersey To Be Shown in Rumson
Survey Will Help Sandy-Affected Towns Address Future Flood Risks

08/26/2014

Survey Will Help Sandy-Affected Towns Address Future Flood Risks
Shared Investment in Urban Water Systems Will Lead to Clean Rivers, More Vibrant Communities

08/25/2014

Shared Investment in Urban Water Systems Will Lead to Clean Rivers, More Vibrant Communities
New Jersey’s Urban Water Systems: A Challenge, and an Opportunity for Collaboration, Engagement, Innovation, Vision

08/04/2014

New Jersey’s Urban Water Systems: A Challenge, and an Opportunity for Collaboration, Engagement, Innovation, Vision
Proposed CAFRA Rule Amendment Increases Dangers from Flooding and Future Storms

08/01/2014

Proposed CAFRA Rule Amendment Increases Dangers from Flooding and Future Storms
New Report Highlights Opportunities To Protect Pinelands Water Resources

07/29/2014

New Report Highlights Opportunities To Protect Pinelands Water Resources
New Draft COAH Rules Ignore Potential of Redevelopment

07/25/2014

New Draft COAH Rules Ignore Potential of Redevelopment
Bell Labs Redevelopment a Sign of the Future

07/24/2014

Bell Labs Redevelopment a Sign of the Future
Hopewell Becomes First Municipality in New Jersey To Adopt Complete Streets Ordinance

07/02/2014

Hopewell Becomes First Municipality in New Jersey To Adopt Complete Streets Ordinance
Hoboken’S Newest Green Infrastructure Project Takes a Step Forward

06/26/2014

Hoboken’S Newest Green Infrastructure Project Takes a Step Forward
Hoboken’s Newest Green Infrastructure Project Takes a Step Forward

06/26/2014

Hoboken’s Newest Green Infrastructure Project Takes a Step Forward
Placing Economic Value on Natural Systems

06/25/2014

Placing Economic Value on Natural Systems
Big Fixes for Water Infrastructure Will Mean Bigger Bills for Customers

06/23/2014

Big Fixes for Water Infrastructure Will Mean Bigger Bills for Customers
Experts Agree on Action Agenda To Address State’s Water Infrastructure Problems

06/18/2014

Experts Agree on Action Agenda To Address State’s Water Infrastructure Problems
Little Egg Harbor, Tuckerton Receive $2.13-Million Resiliency Grant

06/18/2014

Little Egg Harbor, Tuckerton Receive $2.13-Million Resiliency Grant
Innovation Districts: New Jersey Has the Right Ingredients

06/05/2014

Innovation Districts: New Jersey Has the Right Ingredients
Getting to Resilience in Sea Bright

06/03/2014

Getting to Resilience in Sea Bright
Convening Aims to Develop an Agenda for Change for New Jersey’s Urban Water Infrastructure

05/20/2014

Convening Aims to Develop an Agenda for Change for New Jersey’s Urban Water Infrastructure
New Report Highlights State’s Water Infrastructure Crisis

05/16/2014

New Report Highlights State’s Water Infrastructure Crisis
Investing in Transit Is an Economic Incentive

05/14/2014

Investing in Transit Is an Economic Incentive
New Report Highlights State’s Water Infrastructure Crisis

05/06/2014

New Report Highlights State’s Water Infrastructure Crisis
Highlands Development Regulations Not Responsible for Exurban Slowdown

04/24/2014

Highlands Development Regulations Not Responsible for Exurban Slowdown
Forum Plenary: A Tale of Three Cities

04/17/2014

Forum Plenary: A Tale of Three Cities
State Hazard Mitigation Plan Should Do More To Address Risk, Integrate With Local Planning

04/11/2014

State Hazard Mitigation Plan Should Do More To Address Risk, Integrate With Local Planning
Forum Feature: Is Demolition Always the Best Option for Vacant Properties?

04/10/2014

Forum Feature: Is Demolition Always the Best Option for Vacant Properties?
Timing of Public Comment Period on State Hazard Plan Raises Questions

04/04/2014

Timing of Public Comment Period on State Hazard Plan Raises Questions
New County Population Estimates: Older Places Continue Their Revival

04/04/2014

New County Population Estimates: Older Places Continue Their Revival
Communities Need To Understand, Plan Effectively for Climate Risks

04/03/2014

Communities Need To Understand, Plan Effectively for Climate Risks
Forum Feature: Eyes Wide Open or Shut

04/03/2014

Forum Feature: Eyes Wide Open or Shut
2014 Smart Growth Awards Announced

04/01/2014

2014 Smart Growth Awards Announced
A Solution to New Jersey’s Transportation Funding Problem Is on the Horizon

04/01/2014

A Solution to New Jersey’s Transportation Funding Problem Is on the Horizon
Forum Keynote: Target Investments at Assets, not Companies

03/21/2014

Forum Keynote: Target Investments at Assets, not Companies
Forum Feature: Giving Office Parks a New Lease on Life

03/20/2014

Forum Feature: Giving Office Parks a New Lease on Life
Forum Feature: What’s Plan B? Energy Resiliency in Redevelopment

03/20/2014

Forum Feature: What’s Plan B? Energy Resiliency in Redevelopment
Forum Feature: Does Green Infrastructure Create Real Estate Value?

03/20/2014

Forum Feature: Does Green Infrastructure Create Real Estate Value?
Forum Feature: What’s Plan B? Energy Resiliency in Redevelopment

03/20/2014

Forum Feature: What’s Plan B? Energy Resiliency in Redevelopment
Draft 2014 New Jersey Hazard Mitigation Plan Available for Comment

03/11/2014

Draft 2014 New Jersey Hazard Mitigation Plan Available for Comment
NRDC: Risk Assessment Must Be Part of New Jersey’s Sandy Recovery Programs

03/07/2014

NRDC: Risk Assessment Must Be Part of New Jersey’s Sandy Recovery Programs
Advocates Call for Valid Risk Assessment, Mitigation Planning in States Draft Post-Sandy Action Plan

03/05/2014

Advocates Call for Valid Risk Assessment, Mitigation Planning in States Draft Post-Sandy Action Plan
“Shored Up”: An Important Primer on Complex Coastal Development Issues

02/25/2014

“Shored Up”: An Important Primer on Complex Coastal Development Issues
New York State Announces Major Investment in Post-Sandy Community Planning and Implementation

02/20/2014

New York State Announces Major Investment in Post-Sandy Community Planning and Implementation
Report: Many Older New Jerseyans Don’t Live in Aging-Friendly Places

02/18/2014

Report: Many Older New Jerseyans Don’t Live in Aging-Friendly Places
Report: Many Older New Jerseyans Don’t Live in Aging-Friendly Places

02/18/2014

Report: Many Older New Jerseyans Don’t Live in Aging-Friendly Places
New Jersey Must Count the True Costs of Preparing for Sea-Level Rise

02/14/2014

New Jersey Must Count the True Costs of Preparing for Sea-Level Rise
Sprawl Isn’t Dead, It’s Just Hibernating

02/10/2014

Sprawl Isn’t Dead, It’s Just Hibernating
Sprawl Isn’t Dead, It’s Just Hibernating

02/10/2014

Sprawl Isn’t Dead, It’s Just Hibernating
Workshops, Online Feedback Generate Ideas To Help Make Raritan Bay More Resilient

02/07/2014

Workshops, Online Feedback Generate Ideas To Help Make Raritan Bay More Resilient
UPDATED: Three Public Hearings Scheduled on New Sandy Action Plan

02/06/2014

UPDATED: Three Public Hearings Scheduled on New Sandy Action Plan
New CDBG Action Plan Amendment Considers Resiliency

02/04/2014

New CDBG Action Plan Amendment Considers Resiliency
Real Estate Analyst Warns Suburban Land Use Regulations Driving People, Jobs Away

01/29/2014

Real Estate Analyst Warns Suburban Land Use Regulations Driving People, Jobs Away
Is Redevelopment the ‘New Normal?’

01/28/2014

Is Redevelopment the ‘New Normal?’
AIA-NJ Honors New Jersey Future Executive Director

01/28/2014

AIA-NJ Honors New Jersey Future Executive Director
Former New York City Economic Development Head To Deliver Redevelopment Forum Keynote

01/16/2014

Former New York City Economic Development Head To Deliver Redevelopment Forum Keynote
Proposed Sandy Plan Still Puts Taxpayer Dollars at Risk

02/12/2014

Proposed Sandy Plan Still Puts Taxpayer Dollars at Risk
New Jersey Future Offers Grants To Foster Noncontiguous Clustering

11/19/2013

New Jersey Future Offers Grants To Foster Noncontiguous Clustering
Five New Jersey Projects Included in Next Round of HUD’s Rebuild by Design Competition

11/14/2013

Five New Jersey Projects Included in Next Round of HUD’s Rebuild by Design Competition
HUD Releases Notice for Second Round of Sandy Disaster Recovery Funding

11/13/2013

HUD Releases Notice for Second Round of Sandy Disaster Recovery Funding
New Jersey Future Offers Webinar Series, Grant Program for Noncontiguous Cluster Development

11/05/2013

New Jersey Future Offers Webinar Series, Grant Program for Noncontiguous Cluster Development
Nominations Now Open for 2014 Smart Growth Awards

11/04/2013

Nominations Now Open for 2014 Smart Growth Awards
Complete Streets: ‘A Rational Response to Irrational Thinking’

11/01/2013

Complete Streets: ‘A Rational Response to Irrational Thinking’
Lessons From Sandy: Planning for What Lies Ahead

10/30/2013

Lessons From Sandy: Planning for What Lies Ahead
Key Issues: Divergent Views on Jobs and the Economy

10/25/2013

Key Issues: Divergent Views on Jobs and the Economy
Key Issues: Silence on the Environment

10/22/2013

Key Issues: Silence on the Environment
Key Issues: A Hefty Pricetag for Rail Tunnel, Transportation Projects

10/21/2013

Key Issues: A Hefty Pricetag for Rail Tunnel, Transportation Projects
Four Key Issues for New Jersey’s Future

10/20/2013

Four Key Issues for New Jersey’s Future
Four Key Issues for New Jersey’s Future

10/20/2013

Four Key Issues for New Jersey’s Future
Somerset County’s Investment Framework Gets State Planning Commission Support

10/16/2013

Somerset County’s Investment Framework Gets State Planning Commission Support
Somerset County’s Investment Framework Gets State Planning Commission Support

10/16/2013

Somerset County’s Investment Framework Gets State Planning Commission Support
New Report Recommends Regional Coordination, Variety of Coastal Strategies

10/10/2013

New Report Recommends Regional Coordination, Variety of Coastal Strategies
Crowd-Mapping New Jersey’s Growth

10/02/2013

Crowd-Mapping New Jersey’s Growth
State Supreme Court Ruling a Victory for Sound Planning, Housing Affordability

09/26/2013

State Supreme Court Ruling a Victory for Sound Planning, Housing Affordability
Voters in S. Hunterdon Approve Regional School District

09/25/2013

Voters in S. Hunterdon Approve Regional School District
New Legislation Changes the Smart Growth Playing Field

09/18/2013

New Legislation Changes the Smart Growth Playing Field
Five Ways Social Entrepreneurship Could Disrupt Traditional Planning and Development

09/10/2013

Five Ways Social Entrepreneurship Could Disrupt Traditional Planning and Development
Sandy Rebuilding Task Force Issues Recommendations

08/19/2013

Sandy Rebuilding Task Force Issues Recommendations
Governor Signs Bill Improving Municipal Tools for Cluster Development

08/08/2013

Governor Signs Bill Improving Municipal Tools for Cluster Development
New Jersey Experience with Sandy Rebuilding Suggests Ways to Improve Federal Assistance

08/05/2013

New Jersey Experience with Sandy Rebuilding Suggests Ways to Improve Federal Assistance
Upward Economic Mobility Is a Land-Use Issue

08/02/2013

Upward Economic Mobility Is a Land-Use Issue
New Jersey Future Supports Economic Incentives that Don’t Subsidize Sprawl

07/24/2013

New Jersey Future Supports Economic Incentives that Don’t Subsidize Sprawl
New Jersey’s Inner Suburbs: Leading Indicator of Opportunity and Challenge

07/24/2013

New Jersey’s Inner Suburbs: Leading Indicator of Opportunity and Challenge
Post-Sandy Recovery: Balancing Regional Planning With Home Rule

07/23/2013

Post-Sandy Recovery: Balancing Regional Planning With Home Rule
Somerset County Releases Study on Repurposing Under-Utilized Commercial Properties

07/22/2013

Somerset County Releases Study on Repurposing Under-Utilized Commercial Properties
In Rush To Rebuild, Are We Failing To Plan for the Next Superstorm?

07/22/2013

In Rush To Rebuild, Are We Failing To Plan for the Next Superstorm?
Rethinking the Shore Forum Zeroes in on Better Planning, Leadership

07/22/2013

Rethinking the Shore Forum Zeroes in on Better Planning, Leadership
Memo to Municipalities: Get Creative and Flexible if You Want Those Office Parks Redeveloped

07/19/2013

Memo to Municipalities: Get Creative and Flexible if You Want Those Office Parks Redeveloped
Economic Opportunity Act’s “Log Cabin Loophole” Invites Sprawl Subsidies

07/18/2013

Economic Opportunity Act’s “Log Cabin Loophole” Invites Sprawl Subsidies
Economic Opportunity Act’s “Log Cabin Loophole” Invites Sprawl Subsidies

07/18/2013

Economic Opportunity Act’s “Log Cabin Loophole” Invites Sprawl Subsidies
Groups Offer Early Lessons From Post-Sandy Recovery

07/09/2013

Groups Offer Early Lessons From Post-Sandy Recovery
Addressing the Growing Issue of Obsolete Office Parks

07/02/2013

Addressing the Growing Issue of Obsolete Office Parks
New Jersey’s Water Infrastructure: The Biggest Risk Is Doing Nothing

06/25/2013

New Jersey’s Water Infrastructure: The Biggest Risk Is Doing Nothing
Somerset County Forum Highlights Economic Competitiveness Needs

06/18/2013

Somerset County Forum Highlights Economic Competitiveness Needs
Post-Sandy Resiliency Planning Assistance Grants Available

06/17/2013

Post-Sandy Resiliency Planning Assistance Grants Available
Slow Growth, Old Infrastructure Mean a Need for Innovation and Reinvestment

06/13/2013

Slow Growth, Old Infrastructure Mean a Need for Innovation and Reinvestment
Reform Task Force Calls for Large Cut in Property Taxes

06/12/2013

Reform Task Force Calls for Large Cut in Property Taxes
New Jersey Residents Want More Resiliency Post-Sandy, but at No Cost

06/12/2013

New Jersey Residents Want More Resiliency Post-Sandy, but at No Cost
Bill To Increase Aid to Sandy-Stricken Communities Introduced in Congress

06/12/2013

Bill To Increase Aid to Sandy-Stricken Communities Introduced in Congress
Frank Lautenberg, Champion of Smart Growth

06/03/2013

Frank Lautenberg, Champion of Smart Growth
New Report Highlights Fiscal Benefits of Smart-Growth Development

05/21/2013

New Report Highlights Fiscal Benefits of Smart-Growth Development
Redevelopment Forum Approved for Continuing Education Credits

05/16/2013

Redevelopment Forum Approved for Continuing Education Credits
Avoid Penny-wise, Pound-foolish Approach to Resiliency

05/16/2013

Avoid Penny-wise, Pound-foolish Approach to Resiliency
New Jersey Future Receives Housing Award

05/07/2013

New Jersey Future Receives Housing Award
Cluster Development Bill Sails through the Assembly

04/30/2013

Cluster Development Bill Sails through the Assembly
Sandy Recovery Action Plan Doesn’t Commit to Resiliency Planning, Sustainability

04/29/2013

Sandy Recovery Action Plan Doesn’t Commit to Resiliency Planning, Sustainability
Sandy Recovery Action Plan Doesn’t Commit to Resiliency Planning, Sustainability

04/29/2013

Sandy Recovery Action Plan Doesn’t Commit to Resiliency Planning, Sustainability
Regional Planning in the Pinelands: Well-Directed Growth, but What Effect on Natural Resources?

04/11/2013

Regional Planning in the Pinelands: Well-Directed Growth, but What Effect on Natural Resources?
Concern Expressed Over Lack of Planning Funds in Sandy Recovery Action Plan

04/04/2013

Concern Expressed Over Lack of Planning Funds in Sandy Recovery Action Plan
Forum Roundup: The Balancing Act Between Ports and Their Hosts

04/04/2013

Forum Roundup: The Balancing Act Between Ports and Their Hosts
Incorporating Health Into All Policies

04/01/2013

Incorporating Health Into All Policies
Forum Roundup: Creative Housing Solutions for Changing Demographics

03/26/2013

Forum Roundup: Creative Housing Solutions for Changing Demographics
Diane Sterner of Housing and Community Development Network To Receive Leadership Award

03/25/2013

Diane Sterner of Housing and Community Development Network To Receive Leadership Award
Smart Growth Awards 2013 Winners Announced

03/25/2013

Smart Growth Awards 2013 Winners Announced
Forum Roundup: Redeveloping Post-Sandy: Do it Quickly, and Do it Right

03/22/2013

Forum Roundup: Redeveloping Post-Sandy: Do it Quickly, and Do it Right
Clock Is Ticking on Public Comment Period for Sandy Recovery Spending Plan

03/20/2013

Clock Is Ticking on Public Comment Period for Sandy Recovery Spending Plan
Forum Roundup: Auditing New Brunswick’s Walkability

03/19/2013

Forum Roundup: Auditing New Brunswick’s Walkability
Economic Opportunity Act Will Dilute State Incentives and Subsidize Sprawl Unless Amended

03/13/2013

Economic Opportunity Act Will Dilute State Incentives and Subsidize Sprawl Unless Amended
Cluster Development Bill Ready for Full Vote in Senate and Assembly

03/13/2013

Cluster Development Bill Ready for Full Vote in Senate and Assembly
Getting New Jersey Ready To Welcome Green Infrastructure

03/11/2013

Getting New Jersey Ready To Welcome Green Infrastructure
Brownfields Bill BUILDs a Path to Neighborhood Revitalization

03/07/2013

Brownfields Bill BUILDs a Path to Neighborhood Revitalization
Forum Roundup: New Jersey’s Bleak Foreclosure Numbers

03/04/2013

Forum Roundup: New Jersey’s Bleak Foreclosure Numbers
Forum Roundup: The Shaky State of Our Infrastructure

03/04/2013

Forum Roundup: The Shaky State of Our Infrastructure
Forum Roundup: New Jersey’s Bleak Foreclosure Numbers

03/04/2013

Forum Roundup: New Jersey’s Bleak Foreclosure Numbers
Cluster Development Bill Advances

02/27/2013

Cluster Development Bill Advances
So you passed a Complete Streets policy. NOW what?

02/21/2013

So you passed a Complete Streets policy. NOW what?
Market Demand Drives Increase in Multifamily Building Permits in New Jersey

02/20/2013

Market Demand Drives Increase in Multifamily Building Permits in New Jersey
HUD Secretary Donovan To Speak at Redevelopment Forum

02/05/2013

HUD Secretary Donovan To Speak at Redevelopment Forum
Somerset County Pioneers Local Application of State Strategic Plan Investment Criteria

01/31/2013

Somerset County Pioneers Local Application of State Strategic Plan Investment Criteria
Position Available: Recovery Planning Manager

01/30/2013

Position Available: Recovery Planning Manager
Rescheduled Conference Brings Together New Jersey’s Planning Leaders

01/24/2013

Rescheduled Conference Brings Together New Jersey’s Planning Leaders
In Targeting Incentives, Location Matters

01/16/2013

In Targeting Incentives, Location Matters
Blaming the Victim in South Jersey Pedestrian Fatalities

01/03/2013

Blaming the Victim in South Jersey Pedestrian Fatalities
The Coming Boom in White Elephants

01/02/2013

The Coming Boom in White Elephants
Poll Shows New Jersey Residents Strongly Support Regional Approach to Rebuilding After Sandy

12/10/2012

Poll Shows New Jersey Residents Strongly Support Regional Approach to Rebuilding After Sandy
Rebuilding a Resilient Shore Weekly News Roundup Nov. 30, 2012

11/30/2012

Rebuilding a Resilient Shore Weekly News Roundup Nov. 30, 2012
Resilient Shore Daily News Roundup Nov. 21, 2012

11/21/2012

Resilient Shore Daily News Roundup Nov. 21, 2012
Resilience Demonstration Project Assists Four New Jersey Municipalities

11/20/2012

Resilience Demonstration Project Assists Four New Jersey Municipalities
Resilient Shore Daily News Roundup, Nov. 20, 2012

11/20/2012

Resilient Shore Daily News Roundup, Nov. 20, 2012
State Planning Commission Postpones Vote on State Strategic Plan

11/19/2012

State Planning Commission Postpones Vote on State Strategic Plan
Resilient Shore Daily News Roundup, Nov. 19, 2012

11/19/2012

Resilient Shore Daily News Roundup, Nov. 19, 2012
Resilient Shore Daily Roundup, Nov. 15, 2012

11/15/2012

Resilient Shore Daily Roundup, Nov. 15, 2012
Resilient Shore Daily Roundup, Nov. 16, 2012

11/15/2012

Resilient Shore Daily Roundup, Nov. 16, 2012
Resilient Shore Daily Roundup, Nov. 14, 2012

11/14/2012

Resilient Shore Daily Roundup, Nov. 14, 2012
Resilient Shore Daily Roundup, Nov, 13, 2012

11/13/2012

Resilient Shore Daily Roundup, Nov, 13, 2012
Resilient Shore Daily Roundup, Nov. 12, 2012

11/12/2012

Resilient Shore Daily Roundup, Nov. 12, 2012
State Planning Commission To Vote on State Strategic Plan

11/12/2012

State Planning Commission To Vote on State Strategic Plan
25 Years of Smart Growth in New Jersey

11/08/2012

25 Years of Smart Growth in New Jersey
The Jersey Shore: How To Protect a Treasured Asset?

11/02/2012

The Jersey Shore: How To Protect a Treasured Asset?
Planning to Build on Light Rail Success

11/01/2012

Planning to Build on Light Rail Success
TOD Line Newsletter Launched to Highlight TOD Advances and Experiences

10/17/2012

TOD Line Newsletter Launched to Highlight TOD Advances and Experiences
Safe Routes to School: Small Steps for Healthy Kids

10/11/2012

Safe Routes to School: Small Steps for Healthy Kids
Comprehensive Transit Inventory Allows for More Strategic Investment Decisions

09/24/2012

Comprehensive Transit Inventory Allows for More Strategic Investment Decisions
Johnson & Johnson To Establish Innovation Centers

09/19/2012

Johnson & Johnson To Establish Innovation Centers
State Strategic Plan Recognizes Importance of Ports to NJ’s Economy

09/12/2012

State Strategic Plan Recognizes Importance of Ports to NJ’s Economy
Dunellen and East Orange as Transit Villages: One Designation, Two Strategies

08/29/2012

Dunellen and East Orange as Transit Villages: One Designation, Two Strategies
New Jersey State Plan Update Back On Track

08/03/2012

New Jersey State Plan Update Back On Track
Cities (Of All Sizes) Lead the State in Population Growth

07/18/2012

Cities (Of All Sizes) Lead the State in Population Growth
New Sewer Service Maps Will Support Responsible Development, Water Protection

07/17/2012

New Sewer Service Maps Will Support Responsible Development, Water Protection
Urban Transit Hub Tax Credit at a Crossroads

06/28/2012

Urban Transit Hub Tax Credit at a Crossroads
What We Wanted to Say: New Revenue Sources, Not More Borrowing, Needed to Fund Transportation

06/19/2012

What We Wanted to Say: New Revenue Sources, Not More Borrowing, Needed to Fund Transportation
New Jersey Counties Show Dramatic Reversal in Population Growth Patterns

06/12/2012

New Jersey Counties Show Dramatic Reversal in Population Growth Patterns
Does Traffic Congestion Make You More Productive?

06/01/2012

Does Traffic Congestion Make You More Productive?
Seven Exemplary Projects, Plans Earn Smart Growth Awards for 2012

05/31/2012

Seven Exemplary Projects, Plans Earn Smart Growth Awards for 2012
Tangible Progress on Long-Awaited Sewer Service Area Updates

05/31/2012

Tangible Progress on Long-Awaited Sewer Service Area Updates
Milestone No. 2: Ocean County’s Proposed Wastewater Service Areas Published for Review

05/24/2012

Milestone No. 2: Ocean County’s Proposed Wastewater Service Areas Published for Review
New Report: Review of Legal Framework for County Planning in New Jersey

05/21/2012

New Report: Review of Legal Framework for County Planning in New Jersey
Sustainable Sites Can Accommodate New Jersey’s Solar Needs

05/18/2012

Sustainable Sites Can Accommodate New Jersey’s Solar Needs
Walk or Cycle to Work? You Have Company

05/14/2012

Walk or Cycle to Work? You Have Company
Preserving Land through Market Real Estate Transactions: Nine Approaches and Four Success Stories

05/01/2012

Preserving Land through Market Real Estate Transactions: Nine Approaches and Four Success Stories
State Planning Commission Announces Additional Public Hearing for State Strategic Plan

04/30/2012

State Planning Commission Announces Additional Public Hearing for State Strategic Plan
Newark Is Apparently Not a City Either

04/20/2012

Newark Is Apparently Not a City Either
359 Municipalities Working Toward Sustainable Jersey Certification

04/18/2012

359 Municipalities Working Toward Sustainable Jersey Certification
2012 Smart Growth Award Winners Announced

04/18/2012

2012 Smart Growth Award Winners Announced
One-Seat Ride Not Contingent on the (Now-Canceled) ARC Tunnel

04/13/2012

One-Seat Ride Not Contingent on the (Now-Canceled) ARC Tunnel
More New Jersey Commuters Relying on Transit to Get to Work

04/03/2012

More New Jersey Commuters Relying on Transit to Get to Work
New Jersey Future Hails Promise of State Strategic Plan

04/02/2012

New Jersey Future Hails Promise of State Strategic Plan
NJDOT Proposes to Restore Transit Village Program Funding

03/30/2012

NJDOT Proposes to Restore Transit Village Program Funding
State Officials: Redevelopment at the Heart of State Strategic Plan

03/28/2012

State Officials: Redevelopment at the Heart of State Strategic Plan
A Better Transportation Bill

03/22/2012

A Better Transportation Bill
Redevelopment Forum Keynote: Walkable Urbanism Is Key to New Jersey’s Future

03/22/2012

Redevelopment Forum Keynote: Walkable Urbanism Is Key to New Jersey’s Future
What’s Next in the New Jersey Highlands?

03/21/2012

What’s Next in the New Jersey Highlands?
State Planning Commission targets April 25 for State Strategic Plan adoption

03/21/2012

State Planning Commission targets April 25 for State Strategic Plan adoption
New Jersey Isn’t Capitalizing on Demand for Walkable Places

03/05/2012

New Jersey Isn’t Capitalizing on Demand for Walkable Places
Lieutenant Governor To Speak at Redevelopment Forum

02/13/2012

Lieutenant Governor To Speak at Redevelopment Forum
Investment Area Criteria Released for the State Strategic Plan

02/13/2012

Investment Area Criteria Released for the State Strategic Plan
Liveblogging the State Strategic Plan Public Hearing

02/09/2012

Liveblogging the State Strategic Plan Public Hearing
House Transportation Bill Falls Short

02/09/2012

House Transportation Bill Falls Short
Why Hunterdon County Should Regionalize Its School Districts

01/27/2012

Why Hunterdon County Should Regionalize Its School Districts
Does New Jersey Have Room to Grow?

01/26/2012

Does New Jersey Have Room to Grow?
Christie Administration Must Commit to Updating Wastewater Plans

01/19/2012

Christie Administration Must Commit to Updating Wastewater Plans
Our Take on the State of the State Address

01/17/2012

Our Take on the State of the State Address
Is Route 1 a Street or a Road?

01/11/2012

Is Route 1 a Street or a Road?
Public Hearings on State Strategic Plan Begin in February

01/09/2012

Public Hearings on State Strategic Plan Begin in February
Demand Grows for Smart-Growth Work Environments

01/04/2012

Demand Grows for Smart-Growth Work Environments
Rebuilding a Resilient New Jersey Shore Conference Recap

12/13/2012

Rebuilding a Resilient New Jersey Shore Conference Recap
Targeting Industry and Geography Together to Foster Job Growth

09/12/2012

Targeting Industry and Geography Together to Foster Job Growth
Permit Extension Bill Threatens Open Space

12/14/2011

Permit Extension Bill Threatens Open Space
New Jersey Future Seeks Nominations for 2012 Smart Growth Awards

12/09/2011

New Jersey Future Seeks Nominations for 2012 Smart Growth Awards
Byram Township Wins National Smart-Growth Grant

12/09/2011

Byram Township Wins National Smart-Growth Grant
Details on State Strategic Plan Begin to Emerge

12/08/2011

Details on State Strategic Plan Begin to Emerge
Census Data Show Population Growth Has Slowed Across New Jersey

12/01/2011

Census Data Show Population Growth Has Slowed Across New Jersey
Planning Advocates Call For Amendments to Economic Development Bill

12/01/2011

Planning Advocates Call For Amendments to Economic Development Bill
North Jersey Receives $5 Million Federal Grant To Boost Growth Around Transit

11/21/2011

North Jersey Receives $5 Million Federal Grant To Boost Growth Around Transit
Compact Downtown Development Offers Property Tax Benefits

11/17/2011

Compact Downtown Development Offers Property Tax Benefits
Towns Balanced Approach to Transportation Wins Leadership Award

11/17/2011

Towns Balanced Approach to Transportation Wins Leadership Award
Talking About Transportation

11/16/2011

Talking About Transportation
State Planning Commission Releases Draft Final State Plan for Public Hearings

11/14/2011

State Planning Commission Releases Draft Final State Plan for Public Hearings
New Book Offers Regional Planning Solutions That Work

11/14/2011

New Book Offers Regional Planning Solutions That Work
New Jersey Future to Honor Brendan Byrne

11/03/2011

New Jersey Future to Honor Brendan Byrne
Planning Association Conference Includes Sessions on Current Smart-Growth Issues

11/02/2011

Planning Association Conference Includes Sessions on Current Smart-Growth Issues
New: Information Page on the State Strategic Plan

11/01/2011

New: Information Page on the State Strategic Plan
DEP Launches Environmental Management Initiative

10/27/2011

DEP Launches Environmental Management Initiative
Addressing Obesity Through Smart Planning

10/23/2011

Addressing Obesity Through Smart Planning
Christie Releases New State Strategic Plan

10/19/2011

Christie Releases New State Strategic Plan
New Jersey Activists Work to Reverse RGGI Pull-out; New York State Supports ‘Climate-Smart Communities’

10/14/2011

New Jersey Activists Work to Reverse RGGI Pull-out; New York State Supports ‘Climate-Smart Communities’
Proposal Would Reverse Policy of Targeting Energy-Efficiency Incentives to Smart-Growth Areas

10/12/2011

Proposal Would Reverse Policy of Targeting Energy-Efficiency Incentives to Smart-Growth Areas
New Jersey Residents Are Concerned About How the State Has Developed

10/11/2011

New Jersey Residents Are Concerned About How the State Has Developed
County Growth Plans Poised for Adoption

10/05/2011

County Growth Plans Poised for Adoption
The Shadow Northeast Corridor Draws Warehouses and People

10/04/2011

The Shadow Northeast Corridor Draws Warehouses and People
Menendez Focuses on TOD Funding in Updated Livable Communities Act

09/29/2011

Menendez Focuses on TOD Funding in Updated Livable Communities Act
Summit Moves Toward Transit Village Designation, Future of Program Remains Uncertain

09/28/2011

Summit Moves Toward Transit Village Designation, Future of Program Remains Uncertain
We Work Close to Home But We Drive There

09/22/2011

We Work Close to Home But We Drive There
On Balance, New Legislative Effort Keeps Urban Transit Hub Incentives Intact

09/22/2011

On Balance, New Legislative Effort Keeps Urban Transit Hub Incentives Intact
Join us in Supporting the Federal Partnership for Sustainable Communities

09/13/2011

Join us in Supporting the Federal Partnership for Sustainable Communities
Incomplete Report Card for Complete Streets

09/07/2011

Incomplete Report Card for Complete Streets
Zero-Vehicle Households and Transit

09/01/2011

Zero-Vehicle Households and Transit
State Officials Tout Transit Villages

08/25/2011

State Officials Tout Transit Villages
Why Not Tier Solar Incentives to Encourage Advantageous Locations?

08/24/2011

Why Not Tier Solar Incentives to Encourage Advantageous Locations?
Density and Sprawl Are Not Mutually Exclusive

08/24/2011

Density and Sprawl Are Not Mutually Exclusive
What makes a great place to live?

08/19/2011

What makes a great place to live?
How about an E-ZPass for transit?

08/12/2011

How about an E-ZPass for transit?
Accommodating Growth in Mercer County

08/11/2011

Accommodating Growth in Mercer County
Blackouts and a Bright Spot in the Energy Master Plan

08/11/2011

Blackouts and a Bright Spot in the Energy Master Plan
Memo to HR: Want to Attract Top Young Talent in New Jersey? Move to the Cities

08/05/2011

Memo to HR: Want to Attract Top Young Talent in New Jersey? Move to the Cities
New Jersey Dominates List of Top Public Transportation Cities

08/01/2011

New Jersey Dominates List of Top Public Transportation Cities
Highlands Council Can Support Local Growth Plans

08/01/2011

Highlands Council Can Support Local Growth Plans
City-Loving Millennials: Are They Born That Way?

07/28/2011

City-Loving Millennials: Are They Born That Way?
Exclusionary Zoning, Sprawl on the Rise

07/21/2011

Exclusionary Zoning, Sprawl on the Rise
Regional Planning Efforts Have Friends in High Places

07/21/2011

Regional Planning Efforts Have Friends in High Places
New Jersey Cities Breathe Sigh of Relief

07/19/2011

New Jersey Cities Breathe Sigh of Relief
Revision to Land Use Law Advances Smart Growth

07/07/2011

Revision to Land Use Law Advances Smart Growth
New Jersey’s Solar Ambitions Raise Difficult Land-Use Issues

07/06/2011

New Jersey’s Solar Ambitions Raise Difficult Land-Use Issues
Governor Removes Funding for Transit Villages

07/05/2011

Governor Removes Funding for Transit Villages
The Mall as Private City

06/29/2011

The Mall as Private City
Democrats’ Proposed Budget Includes Funding for Transit Village Program

06/27/2011

Democrats’ Proposed Budget Includes Funding for Transit Village Program
Smart Growth Photo Contest

06/26/2011

Smart Growth Photo Contest
Poll Finds Majority Support for Land-Use Policies to Combat Climate Change

06/23/2011

Poll Finds Majority Support for Land-Use Policies to Combat Climate Change
NJ Homebuilders Create Affiliate to Lobby for Multifamily Development

06/20/2011

NJ Homebuilders Create Affiliate to Lobby for Multifamily Development
Bill That Undermines Tax Sharing Passes Committee

06/17/2011

Bill That Undermines Tax Sharing Passes Committee
Jersey City and Ridgewood Adopt Complete Streets Policies, Bringing Statewide Total to 13

06/15/2011

Jersey City and Ridgewood Adopt Complete Streets Policies, Bringing Statewide Total to 13
Metropark, and the Limits of Brookings’ Transit Accessibility Study

06/13/2011

Metropark, and the Limits of Brookings’ Transit Accessibility Study
Mutiny in the Meadowlands

06/11/2011

Mutiny in the Meadowlands
Urban Transit Hub Tax Credit Spurs Development Interest in Newark

06/07/2011

Urban Transit Hub Tax Credit Spurs Development Interest in Newark
New Jersey Future Announces 10th Anniversary Smart Growth Award-Winners

06/03/2011

New Jersey Future Announces 10th Anniversary Smart Growth Award-Winners
Seven Trend-Setting Projects, Plans Earn Smart Growth Awards for 2011

06/01/2011

Seven Trend-Setting Projects, Plans Earn Smart Growth Awards for 2011
Responding to Governor Christie’s Decision to Pull Out of Regional Climate Pact

05/26/2011

Responding to Governor Christie’s Decision to Pull Out of Regional Climate Pact
Many Roads in New Jersey are “Dangerous by Design” for Pedestrians

05/24/2011

Many Roads in New Jersey are “Dangerous by Design” for Pedestrians
National Experts Advise the Christie Administration on State Strategic Planning

05/23/2011

National Experts Advise the Christie Administration on State Strategic Planning
NJDOT Commissioner: $1 Million for Transit Villages Not Enough, So We Made It Zero

05/17/2011

NJDOT Commissioner: $1 Million for Transit Villages Not Enough, So We Made It Zero
Make the Healthy Choice the Easy Choice

05/17/2011

Make the Healthy Choice the Easy Choice
Light Rail Extension to Support TOD in Jersey City

05/13/2011

Light Rail Extension to Support TOD in Jersey City
Deadline Friday – Join Us!

05/12/2011

Deadline Friday – Join Us!
Fear of School Kids Trumps Land-Use Planning in Robbinsville

05/04/2011

Fear of School Kids Trumps Land-Use Planning in Robbinsville
Why NJ Should Tie Business Incentives to Smart Growth

04/26/2011

Why NJ Should Tie Business Incentives to Smart Growth
The Impact of Transit Villages: One Reader’s Story

04/25/2011

The Impact of Transit Villages: One Reader’s Story
Local Agriculture Growing in Popularity and Importance

04/21/2011

Local Agriculture Growing in Popularity and Importance
Controversial Wastewater Deadline Passes

04/08/2011

Controversial Wastewater Deadline Passes
NJ Towns to Compete in New Reality Show: “Ratable Wars”

04/01/2011

NJ Towns to Compete in New Reality Show: “Ratable Wars”
State Reaffirms Commitment to Transit Village Program; Eliminates Funding

03/31/2011

State Reaffirms Commitment to Transit Village Program; Eliminates Funding
A Bleak Recent Past, a Brighter Future Ahead

03/31/2011

A Bleak Recent Past, a Brighter Future Ahead
NJ’s Transportation Capital Plan: Focus on Fix-It-First, Transit, Pedestrian Safety; Transit Villages Slashed

03/28/2011

NJ’s Transportation Capital Plan: Focus on Fix-It-First, Transit, Pedestrian Safety; Transit Villages Slashed
NJ Transit Delays Parking Privatization

03/21/2011

NJ Transit Delays Parking Privatization
2011 Redevelopment Forum SUCCESS!

03/16/2011

2011 Redevelopment Forum SUCCESS!
Pittsburgh Offers Bold Model for Redevelopment

03/16/2011

Pittsburgh Offers Bold Model for Redevelopment
State Launches Strategic State Planning Process

03/10/2011

State Launches Strategic State Planning Process
Bloomfield Adopts Complete Streets Policy

03/08/2011

Bloomfield Adopts Complete Streets Policy
Is Jersey City a Suburb? Joel Kotkin Thinks So.

03/03/2011

Is Jersey City a Suburb? Joel Kotkin Thinks So.
Sweeney: Glassboro to Camden line “will be included” in the Transportation Trust Fund

02/28/2011

Sweeney: Glassboro to Camden line “will be included” in the Transportation Trust Fund
NJ’s Gold Coast Ranks First in “Smart Transportation”

02/25/2011

NJ’s Gold Coast Ranks First in “Smart Transportation”
Forum Puts Focus on Redevelopment

02/24/2011

Forum Puts Focus on Redevelopment
Transit-Accessible Towns In New Jersey Are More Recession-Resistant

02/24/2011

Transit-Accessible Towns In New Jersey Are More Recession-Resistant
New Jer…..

02/22/2011

New Jer…..
New Jersey Leads in Farmland Loss

02/21/2011

New Jersey Leads in Farmland Loss
Governor Vetoes Historic Property Reinvestment Act

02/18/2011

Governor Vetoes Historic Property Reinvestment Act
When it Comes to State Subsidies, Not All Transit Hubs are Equal

02/17/2011

When it Comes to State Subsidies, Not All Transit Hubs are Equal
State Planning Commission Meets for the First Time Since 2009

02/16/2011

State Planning Commission Meets for the First Time Since 2009
Pete Kasabach Discussing Transit-Oriented Development in Jersey City

02/16/2011

Pete Kasabach Discussing Transit-Oriented Development in Jersey City
Fort Monmouth Redevelopment Taking Shape

02/15/2011

Fort Monmouth Redevelopment Taking Shape
Jay Corbalis discussing transportation funding on MY9 News

02/15/2011

Jay Corbalis discussing transportation funding on MY9 News
Another Nail in the McMansion Coffin?

02/14/2011

Another Nail in the McMansion Coffin?
State Planning Commission to Meet on February 16th After Long Hiatus

02/10/2011

State Planning Commission to Meet on February 16th After Long Hiatus
Downtown Revitalization Taking Hold in New Jersey’s Deep South

02/08/2011

Downtown Revitalization Taking Hold in New Jersey’s Deep South
Amtrak, NJ Senators Announce Plans for “New” Tunnel

02/07/2011

Amtrak, NJ Senators Announce Plans for “New” Tunnel
College Students as a Leading Indicator of Diversity

01/31/2011

College Students as a Leading Indicator of Diversity
Nominate Your Favorite New Jersey Project for a Smart Growth Award

01/31/2011

Nominate Your Favorite New Jersey Project for a Smart Growth Award
DEP Decision Sets Positive Precedent for Compact Growth

01/31/2011

DEP Decision Sets Positive Precedent for Compact Growth
Ensuring Roads Fit for All Users

01/20/2011

Ensuring Roads Fit for All Users
Planning Advocacy Head Offers Public Comments, but Few Hints About Future of State Planning

01/19/2011

Planning Advocacy Head Offers Public Comments, but Few Hints About Future of State Planning
BREAKING NEWS: Young People Don’t Want to Live Where Their Parents Did

01/18/2011

BREAKING NEWS: Young People Don’t Want to Live Where Their Parents Did
Historic Preservation Tax Credit Awaits Governor’s Signature

01/14/2011

Historic Preservation Tax Credit Awaits Governor’s Signature
A Look Back at Governor Christie’s First Year

01/13/2011

A Look Back at Governor Christie’s First Year
Christie’s TTF Plan Panned in Print

01/11/2011

Christie’s TTF Plan Panned in Print
New Jersey Future’s Statement on Governor’s TTF Plan

01/07/2011

New Jersey Future’s Statement on Governor’s TTF Plan
“Smart Growth” vs. “Growth Management”

01/06/2011

“Smart Growth” vs. “Growth Management”
Developers Worry Parking Privatization Will Impede TOD…In Boston

01/05/2011

Developers Worry Parking Privatization Will Impede TOD…In Boston
Insights from Review of “The Ethics of Metropolitan Growth”

01/05/2011

Insights from Review of “The Ethics of Metropolitan Growth”
More than 500 registered – join us Friday!

03/02/2011

More than 500 registered – join us Friday!
A Selection of Snippets from 2010 Future Facts

12/28/2010

A Selection of Snippets from 2010 Future Facts
2011 Redevelopment Forum

12/21/2010

2011 Redevelopment Forum
Population Growth Slows in NJ, Nationally

12/21/2010

Population Growth Slows in NJ, Nationally
Cliff Lee Swayed by Philly’s Public Transit?

12/21/2010

Cliff Lee Swayed by Philly’s Public Transit?
National Pundits Weigh in Against NJ Transit Parking Privatization

12/17/2010

National Pundits Weigh in Against NJ Transit Parking Privatization
Planning Groups call for a Full Slate of Committed Nominees to the Highlands Council

12/17/2010

Planning Groups call for a Full Slate of Committed Nominees to the Highlands Council
Governor’s Barnegat Bay Action Plan is a Promising First Step

12/15/2010

Governor’s Barnegat Bay Action Plan is a Promising First Step
Plenty of Room for Growth in Built-Out Communities

12/14/2010

Plenty of Room for Growth in Built-Out Communities
NJ Future Testimony on Affordable Housing Bill

12/14/2010

NJ Future Testimony on Affordable Housing Bill
Extending the No. 7 Train: More Pipe Dream than Panacea

12/09/2010

Extending the No. 7 Train: More Pipe Dream than Panacea
Report Finds Robust Growth in “Built-Out” Towns

12/09/2010

Report Finds Robust Growth in “Built-Out” Towns
Smart Growth Produces Economic Benefits Across the Country

12/02/2010

Smart Growth Produces Economic Benefits Across the Country
Newark to Build New Jersey’s First Protected Bike Lane

11/19/2010

Newark to Build New Jersey’s First Protected Bike Lane
Questions Loom as NJ Transit Considers Privatizing Parking

11/16/2010

Questions Loom as NJ Transit Considers Privatizing Parking
Governance by Watershed: What Would It Look Like in NJ?

11/15/2010

Governance by Watershed: What Would It Look Like in NJ?
What Role Should Stadiums Play in Urban Revitalization?

11/10/2010

What Role Should Stadiums Play in Urban Revitalization?
The End of the ARC Tunnel

10/27/2010

The End of the ARC Tunnel
Smaller Houses: Symptom of the Recession, or Long-Term Trend?

10/26/2010

Smaller Houses: Symptom of the Recession, or Long-Term Trend?
Who Supports ARC?

10/15/2010

Who Supports ARC?
Regional Planning Efforts Deliver Results

10/14/2010

Regional Planning Efforts Deliver Results
Support for ARC Tunnel From Unlikely Sources

10/12/2010

Support for ARC Tunnel From Unlikely Sources
UPDATE: ARC Tunnel Upgraded from Dead to Critical Condition

10/08/2010

UPDATE: ARC Tunnel Upgraded from Dead to Critical Condition
ARC Tunnel is Dead

10/07/2010

ARC Tunnel is Dead
Help Support the ARC Tunnel!

10/05/2010

Help Support the ARC Tunnel!
This Week in Land Use

10/01/2010

This Week in Land Use
Correcting the Record on ARC

09/30/2010

Correcting the Record on ARC
This Week in the ARC Tunnel (again)

09/24/2010

This Week in the ARC Tunnel (again)
New Jersey Future Statement on ARC/TTF Funding

09/20/2010

New Jersey Future Statement on ARC/TTF Funding
This Week in the ARC Tunnel

09/18/2010

This Week in the ARC Tunnel
30 Day Review an Ominous Sign for ARC Tunnel Project

09/15/2010

30 Day Review an Ominous Sign for ARC Tunnel Project
Best Town Name in New Jersey?

09/01/2010

Best Town Name in New Jersey?
Two More Communities Adopt Complete Streets Policies, More Likely

08/25/2010

Two More Communities Adopt Complete Streets Policies, More Likely
Sustainable Communities: The Light at the End of the Tunnel

08/24/2010

Sustainable Communities: The Light at the End of the Tunnel
Municipal Ratables Chase Doesn’t Necessarily Pay

08/04/2010

Municipal Ratables Chase Doesn’t Necessarily Pay
NJ Future on WNYC’s Brian Lehrer Show

08/03/2010

NJ Future on WNYC’s Brian Lehrer Show
RPA Report Finds ARC To Raise Home Values By $18 Billion

07/30/2010

RPA Report Finds ARC To Raise Home Values By $18 Billion
Sprawl Not Yet a Thing of the Past

07/29/2010

Sprawl Not Yet a Thing of the Past
New Report Shows Suburbanization of NJ Has Picked Up Pace Since 2002

07/28/2010

New Report Shows Suburbanization of NJ Has Picked Up Pace Since 2002
Monmouth County, West Windsor Twp Adopt Complete Streets Policies

07/26/2010

Monmouth County, West Windsor Twp Adopt Complete Streets Policies
Walkable, Transit-Rich Neighborhoods Poised for Comeback

07/23/2010

Walkable, Transit-Rich Neighborhoods Poised for Comeback
Lieutenant Governor Announces New State Office of Planning Advocacy

07/23/2010

Lieutenant Governor Announces New State Office of Planning Advocacy
Urban Centers Weathering Economic Storm Better Than Other Places?

07/08/2010

Urban Centers Weathering Economic Storm Better Than Other Places?
New Tunnel Could Transform NJs Landscape And Brighten its Economic Prospects

07/06/2010

New Tunnel Could Transform NJs Landscape And Brighten its Economic Prospects
DEP Announces New Initiative to Combat Transportation Emissions

06/18/2010

DEP Announces New Initiative to Combat Transportation Emissions
If New Jersey Were a Country

06/17/2010

If New Jersey Were a Country
This Week in Transportation

06/17/2010

This Week in Transportation
New Jersey Future Statement on S1

06/10/2010

New Jersey Future Statement on S1
Could NJ’s Depleted Trust Fund Jeopardize Federal Funding for ARC?

06/09/2010

Could NJ’s Depleted Trust Fund Jeopardize Federal Funding for ARC?
Trenton and Jersey City Receive HOPE VI grants from HUD

06/02/2010

Trenton and Jersey City Receive HOPE VI grants from HUD
Smart Growth Award-Winners Show Innovation, Creativity

05/26/2010

Smart Growth Award-Winners Show Innovation, Creativity
NJ Sens. Menendez and Lautenberg Introduce Emergency Transit Funding Bill

05/25/2010

NJ Sens. Menendez and Lautenberg Introduce Emergency Transit Funding Bill
NJ Ranked as 8th Friendliest State for Bicyclists

05/24/2010

NJ Ranked as 8th Friendliest State for Bicyclists
State Affirms Support—But No Money—for PATCO Extension

05/14/2010

State Affirms Support—But No Money—for PATCO Extension
State and Federal Initiatives Raise Difficult Questions about Solar Siting

05/13/2010

State and Federal Initiatives Raise Difficult Questions about Solar Siting
Parking at NJ Transit Stations Can Generate More than Revenue

05/12/2010

Parking at NJ Transit Stations Can Generate More than Revenue
Tell NJ’s Senators to Stand up for Transit Riders in New Jersey!

05/11/2010

Tell NJ’s Senators to Stand up for Transit Riders in New Jersey!
2010 Smart Growth Awards

05/06/2010

2010 Smart Growth Awards
Christie’s Red Tape panel deserves praise for recommending a shakeup of N.J. planning process

05/03/2010

Christie’s Red Tape panel deserves praise for recommending a shakeup of N.J. planning process
By the Numbers: County Population Estimates Defy Earlier Trends

04/28/2010

By the Numbers: County Population Estimates Defy Earlier Trends
Non-English-Speakers More Common in NJ than Nationally

04/27/2010

Non-English-Speakers More Common in NJ than Nationally
Menendez Introduces Bill to Provide Tax Credit for Transit Oriented Development, But Will the Zoning Be There?

04/26/2010

Menendez Introduces Bill to Provide Tax Credit for Transit Oriented Development, But Will the Zoning Be There?
Uncertain Future for Trust Fund, PATCO Extension at Transportation Hearing

04/22/2010

Uncertain Future for Trust Fund, PATCO Extension at Transportation Hearing
Celebrate Earth Day on Two Wheels or Two Feet

04/22/2010

Celebrate Earth Day on Two Wheels or Two Feet
Metro Areas Are the Key to America’s – and New Jersey’s – Future Economic Prosperity

04/22/2010

Metro Areas Are the Key to America’s – and New Jersey’s – Future Economic Prosperity
Red Tape Review Calls for Moving, Strengthening State Planning Commission and Office of Smart Growth

04/20/2010

Red Tape Review Calls for Moving, Strengthening State Planning Commission and Office of Smart Growth
“Unpredictability” Tops List of Impediments to Redevelopment According to Forum Attendees

04/19/2010

“Unpredictability” Tops List of Impediments to Redevelopment According to Forum Attendees
New Jersey Future Announces Smart Growth Award Winners for 2010

04/16/2010

New Jersey Future Announces Smart Growth Award Winners for 2010
Urban Centers on Rebound

04/09/2010

Urban Centers on Rebound
NJDOT Commissioner Calls for Dedicated Funding For NJ Transit from Turnpike Tolls

04/05/2010

NJDOT Commissioner Calls for Dedicated Funding For NJ Transit from Turnpike Tolls
NJ Transit Introduces “Outdoor Seating” As New, Affordable Option for Riders

04/01/2010

NJ Transit Introduces “Outdoor Seating” As New, Affordable Option for Riders
T4 America Study Finds Americans Support Increased Funding for Public Transportation, Safe Walking and Bicycling

03/31/2010

T4 America Study Finds Americans Support Increased Funding for Public Transportation, Safe Walking and Bicycling
EPA Study Finds Redevelopment Taking Hold Nationwide, What About NJ?

03/30/2010

EPA Study Finds Redevelopment Taking Hold Nationwide, What About NJ?
Demographic Changes May Mean Big Redevelopment Opportunities

03/25/2010

Demographic Changes May Mean Big Redevelopment Opportunities
Transportation Trust Fund on the Road to Bankruptcy

03/11/2010

Transportation Trust Fund on the Road to Bankruptcy
Support for Gas Tax from a Surprising Source

03/10/2010

Support for Gas Tax from a Surprising Source
Fare Hikes and Service Cuts Announced for NJ Transit

03/05/2010

Fare Hikes and Service Cuts Announced for NJ Transit
Poll Shows New Jersey Residents Concerned About Transportation Funding

03/01/2010

Poll Shows New Jersey Residents Concerned About Transportation Funding
Market Forces Portend Shift From Sprawl to Redevelopment

02/18/2010

Market Forces Portend Shift From Sprawl to Redevelopment
Stimulus Investment in Transit Creates Twice as Many Jobs as Roads

02/17/2010

Stimulus Investment in Transit Creates Twice as Many Jobs as Roads
Budget Ax Falls on Transit, Spares Roads

02/16/2010

Budget Ax Falls on Transit, Spares Roads
Groups to Governor Christie: No Cuts to Transit!

02/11/2010

Groups to Governor Christie: No Cuts to Transit!
Governor’s Housing Opportunity Task Force to Assess State Planning Act

02/11/2010

Governor’s Housing Opportunity Task Force to Assess State Planning Act
Are Transit Cuts in Salem a Sign of Things to Come for NJ?

02/05/2010

Are Transit Cuts in Salem a Sign of Things to Come for NJ?
With Release of Impact Assessment, State Plan Poised for Revision, Re-adoption

01/29/2010

With Release of Impact Assessment, State Plan Poised for Revision, Re-adoption
2010 Redevelopment Forum Sponsorships

01/28/2010

2010 Redevelopment Forum Sponsorships
NJ Cities Dominate the Car-Free List – But for the Right Reasons?

01/21/2010

NJ Cities Dominate the Car-Free List – But for the Right Reasons?
Challenges Abound, Opportunity Knocks as Christie Prepares to Take Office

01/14/2010

Challenges Abound, Opportunity Knocks as Christie Prepares to Take Office
Should we be happy or sad about fewer people on the road?

01/11/2010

Should we be happy or sad about fewer people on the road?
Taxes Chasing People Out of New Jersey – But Which Tax? And Which People?

02/10/2010

Taxes Chasing People Out of New Jersey – But Which Tax? And Which People?
New Jersey Embraces Smart Growth to Combat Climate Change

12/23/2009

New Jersey Embraces Smart Growth to Combat Climate Change
Smart Growth in Transition Part V: Property Taxes

12/22/2009

Smart Growth in Transition Part V: Property Taxes
Smart Growth in Transition Part IV: Affordable Housing

12/17/2009

Smart Growth in Transition Part IV: Affordable Housing
Smart Growth in Transition-Part III: Urban Revitalization

12/04/2009

Smart Growth in Transition-Part III: Urban Revitalization
Smart Growth in Transition, Part II: Transportation

11/25/2009

Smart Growth in Transition, Part II: Transportation
Smart Growth in Transition, Part I: State Planning

11/17/2009

Smart Growth in Transition, Part I: State Planning
What Will Smart Growth Look Like in a Christie Administration?

11/04/2009

What Will Smart Growth Look Like in a Christie Administration?
Study Confirms Need to Put Teeth Behind State Smart Growth Plans

11/03/2009

Study Confirms Need to Put Teeth Behind State Smart Growth Plans
Update from Washington

10/29/2009

Update from Washington
What People Think About State Planning in New Jersey

10/27/2009

What People Think About State Planning in New Jersey
New Jersey Future Supports Bond Issue

10/26/2009

New Jersey Future Supports Bond Issue
Star-Ledger on Complete Streets

10/19/2009

Star-Ledger on Complete Streets
Gubernatorial Candidates Weigh In on Smart Growth

10/15/2009

Gubernatorial Candidates Weigh In on Smart Growth
Letter to Gubernatorial Candidates

10/15/2009

Letter to Gubernatorial Candidates
Groups: New Jersey Needs a Complete Streets Policy

10/13/2009

Groups: New Jersey Needs a Complete Streets Policy
New Jersey Future on WNYC

10/09/2009

New Jersey Future on WNYC
Where and How is New Jersey Growing?

10/08/2009

Where and How is New Jersey Growing?
Statement from New Jersey Future on State Planning Act

10/05/2009

Statement from New Jersey Future on State Planning Act
New Jersey Future in the Star-Ledger

10/01/2009

New Jersey Future in the Star-Ledger
Congressman Holt Joins Daily Commute For ‘Take Your Legislator To Work Day

09/30/2009

Congressman Holt Joins Daily Commute For ‘Take Your Legislator To Work Day
State Planning: A Picture of Neglect

09/28/2009

State Planning: A Picture of Neglect
Regional Impact, Local Decision

09/27/2009

Regional Impact, Local Decision
Room with a View

09/27/2009

Room with a View
Menendez Co-Sponsors TOD Bill

09/27/2009

Menendez Co-Sponsors TOD Bill
From the South Jersey Desk

09/27/2009

From the South Jersey Desk
Agriculture Means Business in New Jersey

08/19/2009

Agriculture Means Business in New Jersey
Cities Show Signs of Reversing Trend, Gaining Population

07/15/2009

Cities Show Signs of Reversing Trend, Gaining Population
Statewide Smart Growth Policies Make a Difference

07/01/2009

Statewide Smart Growth Policies Make a Difference
Federal Transportation Spending Bill Has Great Potential

06/24/2009

Federal Transportation Spending Bill Has Great Potential
Economic Stimulus Bill Requires Transparency, Strategic Focus

06/18/2009

Economic Stimulus Bill Requires Transparency, Strategic Focus
Seven Innovative Projects Win Smart Growth Awards

06/01/2009

Seven Innovative Projects Win Smart Growth Awards
Complete Streets Accommodate All Users

05/20/2009

Complete Streets Accommodate All Users
Suburbs Still Growing … But So Are The Cities

05/04/2009

Suburbs Still Growing … But So Are The Cities
On Earth Day, Taking Stock of New Jersey’s Environmental Record

04/20/2009

On Earth Day, Taking Stock of New Jersey’s Environmental Record
Where Jobs Have Gone, Affordable Housing Hasn’t

04/03/2009

Where Jobs Have Gone, Affordable Housing Hasn’t
State Plan offers Clear Path for PATCO Rail Line Extension

03/18/2009

State Plan offers Clear Path for PATCO Rail Line Extension
Redevelopment Offers Antidote to Sprawl

03/04/2009

Redevelopment Offers Antidote to Sprawl
Agreement on Waterfront Plan Buoys Redevelopment in Trenton

02/18/2009

Agreement on Waterfront Plan Buoys Redevelopment in Trenton
Redevelopment Offers Towns Opportunity

02/04/2009

Redevelopment Offers Towns Opportunity
NJ Can Brighten its Future by Stretching Stimulus Dollars

01/15/2009

NJ Can Brighten its Future by Stretching Stimulus Dollars
A Collection of Snippets from 2008 Future Facts

12/31/2008

A Collection of Snippets from 2008 Future Facts
Smart Housing Incentives Legislation Introduced

12/17/2008

Smart Housing Incentives Legislation Introduced
Where and How We Develop is Key to Reducing Greenhouse Gas Emissions

12/05/2008

Where and How We Develop is Key to Reducing Greenhouse Gas Emissions
NJ Should Get to Work Making it Easier to Get to Work

11/24/2008

NJ Should Get to Work Making it Easier to Get to Work
Light Rail Spurs Smart Growth and Property Values Skyrocket

11/03/2008

Light Rail Spurs Smart Growth and Property Values Skyrocket
First-Time Homebuyers, Renters May Be Priced Out Of NJ

10/21/2008

First-Time Homebuyers, Renters May Be Priced Out Of NJ
Tolls and Transit: Perfect Together?

10/06/2008

Tolls and Transit: Perfect Together?
More than Money Needed to Meet Farmland Preservation Goals

09/22/2008

More than Money Needed to Meet Farmland Preservation Goals
Schools Should be Prime Target for Realignment

09/05/2008

Schools Should be Prime Target for Realignment
Sprawl Continues to Consume New Jersey’s Open Lands

08/06/2008

Sprawl Continues to Consume New Jersey’s Open Lands
NJ is Well-Equipped for – But Not Always Open to – TOD

07/17/2008

NJ is Well-Equipped for – But Not Always Open to – TOD
In Large Metro Areas, It’s Easy Being Green

07/02/2008

In Large Metro Areas, It’s Easy Being Green
Permit Extension – A Balancing Act

06/13/2008

Permit Extension – A Balancing Act
NJ Embraces Smart Growth, and Honors those Who Practice It

06/02/2008

NJ Embraces Smart Growth, and Honors those Who Practice It
Report Outlines Agenda for Urban Transformation

05/15/2008

Report Outlines Agenda for Urban Transformation
Housing Costs, Property Taxes Shift Along with Population

05/07/2008

Housing Costs, Property Taxes Shift Along with Population
One Township Blazes a Trail but the State Must Help it Along

04/14/2008

One Township Blazes a Trail but the State Must Help it Along
Fighting Climate Change Starts at Home

04/04/2008

Fighting Climate Change Starts at Home
Higher Gas Prices are on the Horizon but NJ is Well-Positioned to Weather Storm

03/19/2008

Higher Gas Prices are on the Horizon but NJ is Well-Positioned to Weather Storm
Redevelopment: A Blueprint for Sustainability

03/06/2008

Redevelopment: A Blueprint for Sustainability
New Jersey’s Hidden Economic Strengths

02/26/2008

New Jersey’s Hidden Economic Strengths
Leed-ND: A New Framework for Sustainable Development

02/20/2008

Leed-ND: A New Framework for Sustainable Development
Financial Restructuring: Cash Today, Tolls Tomorrow

01/17/2008

Financial Restructuring: Cash Today, Tolls Tomorrow
2007 Year in Review

12/28/2007

2007 Year in Review
A Fresh Look at Affordable Housing

12/19/2007

A Fresh Look at Affordable Housing
Brownfields: Urban Blight or Redevelopment Opportunity?

12/07/2007

Brownfields: Urban Blight or Redevelopment Opportunity?
NJ Still Has Room to Grow. But Where…and How?

11/20/2007

NJ Still Has Room to Grow. But Where…and How?
Preserving NJ’s Landscape is a Daunting Challenge

10/31/2007

Preserving NJ’s Landscape is a Daunting Challenge
Trash and Landfills-A Smart Land Use?

10/16/2007

Trash and Landfills-A Smart Land Use?
Taxes, Infrastructure Repair, and Lane Use

10/03/2007

Taxes, Infrastructure Repair, and Lane Use
Updated Census Numbers Deliver Mixed Message to NJ

09/18/2007

Updated Census Numbers Deliver Mixed Message to NJ
Transit, Past and Future?

08/24/2007

Transit, Past and Future?
In Search of a Balance between Property Rights and Redevelopment

07/27/2007

In Search of a Balance between Property Rights and Redevelopment
The Link Between Energy Use and Land Use

06/19/2007

The Link Between Energy Use and Land Use
TDR Implementation – Keen Interest, Slow Progress

06/01/2007

TDR Implementation – Keen Interest, Slow Progress
Old Cities, New Potential?

05/16/2007

Old Cities, New Potential?
New Sewer Rules, New Hope for Smart Growth?

05/02/2007

New Sewer Rules, New Hope for Smart Growth?
Washington Township and Smart Growth

04/17/2007

Washington Township and Smart Growth
South Jersey: A New Smart Growth Frontier?

04/07/2007

South Jersey: A New Smart Growth Frontier?
COAH Ruling Ignores today’s Affordable Housing Needs

03/15/2007

COAH Ruling Ignores today’s Affordable Housing Needs
Redevelopment on the Rise

02/20/2007

Redevelopment on the Rise
RCA’s: More Harm Than Good?

01/31/2007

RCA’s: More Harm Than Good?
Tax Relief without Reform?

01/12/2007

Tax Relief without Reform?
2006 Year in Review

12/28/2006

2006 Year in Review
Can Property Tax Relief Help Slow Sprawl?

12/18/2006

Can Property Tax Relief Help Slow Sprawl?
Cashing in on History

11/28/2006

Cashing in on History
Fewer Kids Living in Transit Villages and Town Homes

11/26/2006

Fewer Kids Living in Transit Villages and Town Homes
Voting for Property Tax Relief or Reform?

11/03/2006

Voting for Property Tax Relief or Reform?
Voting for Parks

10/20/2006

Voting for Parks
Nowhere to Live

09/29/2006

Nowhere to Live
Seeking a Prosperous Garden State

09/14/2006

Seeking a Prosperous Garden State
Growing Smart and Water Wise

08/31/2006

Growing Smart and Water Wise
Thinking “Outside of the Curbs”

06/21/2006

Thinking “Outside of the Curbs”
The Leaders in Economic Development

05/31/2006

The Leaders in Economic Development
Gas Prices and Smart Growth

05/16/2006

Gas Prices and Smart Growth
Prosperity at Risk

04/21/2006

Prosperity at Risk
Greener Pastures Outside Garden State?

03/31/2006

Greener Pastures Outside Garden State?
Catalysts for Urban Change

03/17/2006

Catalysts for Urban Change
New Jersey’s Five-Year Plan

03/06/2006

New Jersey’s Five-Year Plan
The Real Gripe about Gas Tax

02/16/2006

The Real Gripe about Gas Tax
Sprawling Migration Patterns

01/31/2006

Sprawling Migration Patterns
The Property Tax Problem

07/28/2006

The Property Tax Problem
2005 Year in Review

12/29/2005

2005 Year in Review
Baby Boomers Turn 60

12/19/2005

Baby Boomers Turn 60
Daytime Population Booms

11/30/2005

Daytime Population Booms
Global Warming and New Jersey Development

11/18/2005

Global Warming and New Jersey Development
Open Space Ballots

10/31/2005

Open Space Ballots
The Gubernatorial Race

10/21/2005

The Gubernatorial Race
State Plan Update Still Stalled

09/30/2005

State Plan Update Still Stalled
Marooned Without Options

09/19/2005

Marooned Without Options
Going the Distance

08/31/2005

Going the Distance
Saving Money by Choice

06/30/2005

Saving Money by Choice
Land Use and Equity

05/31/2005

Land Use and Equity
Supporting Tax Relief, But Not Reform?

05/13/2005

Supporting Tax Relief, But Not Reform?
Voters: Give Use Redevelopment

04/29/2005

Voters: Give Use Redevelopment
Eminent Domain and Redevelopment

04/15/2005

Eminent Domain and Redevelopment
Pacesetters in Historic Preservation

03/04/2005

Pacesetters in Historic Preservation
Preservation Challenge for Highlands

02/18/2005

Preservation Challenge for Highlands
Family Unfriendly towns

01/28/2005

Family Unfriendly towns
The Governor’s Priorities

01/07/2005

The Governor’s Priorities
Urban Turnaround

07/29/2005

Urban Turnaround
2004 Year in Review

12/20/2004

2004 Year in Review
TDR Nears Home Stretch

12/12/2004

TDR Nears Home Stretch
New Jersey’s Mean Streets

12/03/2004

New Jersey’s Mean Streets
Transit Popularity Driving Housing Demand

11/19/2004

Transit Popularity Driving Housing Demand
Less Sprawl = Better Health

11/05/2004

Less Sprawl = Better Health
Protecting New Jersey’s Past, Present and Future

10/22/2004

Protecting New Jersey’s Past, Present and Future
Concentrating Poverty

10/08/2004

Concentrating Poverty
Uncovering the Real Need for Affordable Housing

09/20/2004

Uncovering the Real Need for Affordable Housing
Smart Conservation and Density

08/10/2004

Smart Conservation and Density
Mixed Use and Smart Downtowns

07/20/2004

Mixed Use and Smart Downtowns
Transit: A Real Home Advance

06/30/2004

Transit: A Real Home Advance
Gardens Leaving Garden State

06/11/2004

Gardens Leaving Garden State
Sprawl Continues Apace

06/01/2004

Sprawl Continues Apace
Rethinking Oil Consumption

05/21/2004

Rethinking Oil Consumption
Census Confirms Highlands Growth Pressures

04/30/2004

Census Confirms Highlands Growth Pressures
Stranded Without Options

04/20/2004

Stranded Without Options
Less Housing, Higher Prices

03/18/2004

Less Housing, Higher Prices
10,000 Steps and Smarter Growth

03/02/2004

10,000 Steps and Smarter Growth
Growth and the Highlands

02/13/2004

Growth and the Highlands
Making Redevelopment Easier

01/30/2004

Making Redevelopment Easier
Seeking Smart Growth Momentum

01/19/2004

Seeking Smart Growth Momentum
2003 Year in Review

12/31/2003

2003 Year in Review
Gas Tax Too Expensive

11/26/2003

Gas Tax Too Expensive
New Way to Pay for Schools

11/14/2003

New Way to Pay for Schools
Big Map Bows to State Plan

10/24/2003

Big Map Bows to State Plan
Making New Jersey “Clean and Green”

10/11/2003

Making New Jersey “Clean and Green”
Open Space Action Needed

09/23/2003

Open Space Action Needed
State Misses Lead in Affordable Housing

07/31/2003

State Misses Lead in Affordable Housing
Saving New Jersey’s Heritage

07/20/2003

Saving New Jersey’s Heritage
Report: Few Escape Negative Impacts of Sprawl

06/20/2003

Report: Few Escape Negative Impacts of Sprawl
A Housing Dilemma

06/05/2003

A Housing Dilemma
Market Needs Vs. Housing Choice

05/16/2003

Market Needs Vs. Housing Choice
The Conservation Challenge

04/18/2003

The Conservation Challenge
Development and Transit Towns

03/31/2003

Development and Transit Towns
Impact Fees and Sprawl

03/21/2003

Impact Fees and Sprawl
Finding Room for 1 Million New Residents

02/28/2003

Finding Room for 1 Million New Residents
Saving on Gas By Design

02/13/2003

Saving on Gas By Design
State Budgets and Spending For Development

01/31/2003

State Budgets and Spending For Development
Cyanamid Site and Tax-Sharing

12/13/2002

Cyanamid Site and Tax-Sharing
Buying Land Not Only Way to Protect It

11/14/2002

Buying Land Not Only Way to Protect It
Protecting the Highlands

11/14/2002

Protecting the Highlands
Summit Touches Key Causes of Sprawl

10/31/2002

Summit Touches Key Causes of Sprawl
Governor Sets Summit for October 22

10/11/2002

Governor Sets Summit for October 22
Sprawl and Drought

09/25/2002

Sprawl and Drought
New Jersey’s Labor Force

08/30/2002

New Jersey’s Labor Force
NJ Out of Line in School Spending, Funding

08/16/2002

NJ Out of Line in School Spending, Funding
Affordable Housing and Sprawl

08/02/2002

Affordable Housing and Sprawl
McMansions Rise, Along With Overcrowding

07/12/2002

McMansions Rise, Along With Overcrowding
Urbanization Continues to Overrun Borders

06/22/2002

Urbanization Continues to Overrun Borders
NJ Housing Even Less Affordable

05/17/2002

NJ Housing Even Less Affordable
Lake Tahoe Ripples Reach New Jersey

04/30/2002

Lake Tahoe Ripples Reach New Jersey
Council Kicks Off April 23

04/19/2002

Council Kicks Off April 23
Property Tax System Broken, Too

03/26/2002

Property Tax System Broken, Too
Transit Towns Good Places To Grow

03/08/2002

Transit Towns Good Places To Grow
Leaders of the Pack

02/18/2002

Leaders of the Pack
The Housing Hunt

01/23/2002

The Housing Hunt
A Step Away from Cleaner Water

01/10/2002

A Step Away from Cleaner Water
Real Winter Warmth?

12/11/2001

Real Winter Warmth?
New Taxes or No, Tax System Needs Repair

11/30/2001

New Taxes or No, Tax System Needs Repair
New Priorities Call For Better Coordination, Oversight of Planning

10/31/2001

New Priorities Call For Better Coordination, Oversight of Planning
Farmland Tax Policies Work Against Preservation

10/10/2001

Farmland Tax Policies Work Against Preservation
Building Stronger Communities by Tax Sharing

09/20/2001

Building Stronger Communities by Tax Sharing
Grade-A Idea Gets A Pass From New Jersey

08/31/2001

Grade-A Idea Gets A Pass From New Jersey
No Borrowing, Just New Priorities, Could Fund Redevelopment

08/17/2001

No Borrowing, Just New Priorities, Could Fund Redevelopment
Saving Land Without The Tax Bite Takes TDRs

08/01/2001

Saving Land Without The Tax Bite Takes TDRs
State Needs New Water Rules Tied To Growth

07/12/2001

State Needs New Water Rules Tied To Growth
Healthiest Gains Come From Walkable Communities

06/28/2001

Healthiest Gains Come From Walkable Communities
Planning Trumps Size When It Comes To Traffic

05/31/2001

Planning Trumps Size When It Comes To Traffic
Increasing Mom’s Choice of Where To Live

05/11/2001

Increasing Mom’s Choice of Where To Live
NJ Needs Stable Source of Funding for Redevelopment

04/30/2001

NJ Needs Stable Source of Funding for Redevelopment
Sprawl Gets NJ Coming and Going via Property Tax

03/30/2001

Sprawl Gets NJ Coming and Going via Property Tax
New Jersey’s “Principal Cities” Now Include Suburbs

03/14/2001

New Jersey’s “Principal Cities” Now Include Suburbs
Development Style Can Reduce Road Costs

02/13/2001

Development Style Can Reduce Road Costs
If You Zone For It, They Will Come

01/25/2001

If You Zone For It, They Will Come
Property Taxes Drive Urban Distress and Sprawl

01/10/2001

Property Taxes Drive Urban Distress and Sprawl
Municipalities Need a “Smart Growth Shield”

06/19/2001

Municipalities Need a “Smart Growth Shield”
Where Do We Go From Here?

12/22/2000

Where Do We Go From Here?
NJ’s Dirty Secret – Not Enough Housing Affordable To NJ’s Workers

12/08/2000

NJ’s Dirty Secret – Not Enough Housing Affordable To NJ’s Workers
New Housing

11/27/2000

New Housing
The Maryland Approach

11/08/2000

The Maryland Approach
The Minnesota Approach

10/23/2000

The Minnesota Approach
The Oregon Approach

10/05/2000

The Oregon Approach
Suburbs Slipping into Hole of Urban Decline

09/22/2000

Suburbs Slipping into Hole of Urban Decline
Lessons from a Poster Child

09/01/2000

Lessons from a Poster Child
Population Swells Demand for Redevelopment

08/18/2000

Population Swells Demand for Redevelopment
Zoned for Development

07/10/2000

Zoned for Development
Wastewater Rules to Change Development

06/19/2000

Wastewater Rules to Change Development
Voters Taking Different Track

06/02/2000

Voters Taking Different Track
Tougher Shore Development Rules Face Setback

05/15/2000

Tougher Shore Development Rules Face Setback
Senate Bill On Track Toward Smart Growth

05/03/2000

Senate Bill On Track Toward Smart Growth

Power Our Progress

Your generous support is essential to our mission. It fuels the research, advocacy, and on-the-ground assistance we provide to communities, helping to create a more equitable, resilient, and prosperous New Jersey for all.

 

 

Donate Today
Power Our Progress